Trigonometria, si shkencë, e ka origjinën në Lindjen e Lashtë. Raportet e para trigonometrike u përftuan nga astronomët për të krijuar një kalendar dhe orientim të saktë nga yjet. Këto llogaritje kanë të bëjnë me trigonometrinë sferike, ndërsa në kursin e shkollës studiohen raporti i brinjëve dhe këndeve të një trekëndëshi të rrafshët.
Trigonometria është një degë e matematikës që merret me vetitë e funksioneve trigonometrike dhe marrëdhëniet ndërmjet brinjëve dhe këndeve të trekëndëshave.
Gjatë lulëzimit të kulturës dhe shkencës në mijëvjeçarin I pas Krishtit, njohuritë u përhapën nga Lindja e Lashtë në Greqi. Por zbulimet kryesore të trigonometrisë janë meritë e njerëzve të Kalifatit Arab. Në veçanti, shkencëtari turkmen al-Marazwi prezantoi funksione të tilla si tangjentja dhe kotangjentja, dhe përpiloi tabelat e para të vlerave për sinuset, tangjentet dhe kotangjentet. Konceptet e sinusit dhe kosinusit u prezantuan nga shkencëtarët indianë. Trigonometria mori shumë vëmendje në veprat e figurave të tilla të mëdha të antikitetit si Euklidi, Arkimedi dhe Eratostheni.
Madhësitë themelore të trigonometrisë
Funksionet bazë trigonometrike të një argumenti numerik janë sinusi, kosinusi, tangjentja dhe kotangjentja. Secila prej tyre ka grafikun e vet: sinus, kosinus, tangjent dhe kotangjent.
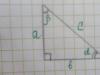
Formulat për llogaritjen e vlerave të këtyre sasive bazohen në teoremën e Pitagorës. Është më mirë e njohur për nxënësit e shkollës në formulimin: "Pantallonat e Pitagorës janë të barabarta në të gjitha drejtimet", pasi prova është dhënë duke përdorur shembullin e një trekëndëshi kënddrejtë izosceles.
Sinus, kosinus dhe marrëdhënie të tjera vendosin marrëdhëniet midis këndeve akute dhe brinjëve të çdo trekëndëshi kënddrejtë. Le të paraqesim formulat për llogaritjen e këtyre sasive për këndin A dhe të gjurmojmë marrëdhëniet midis funksioneve trigonometrike:

Siç mund ta shihni, tg dhe ctg janë funksione të anasjellta. Nëse e imagjinojmë këmbën a si produkt të mëkatit A dhe hipotenuzës c, dhe këmbën b si cos A * c, marrim formulat e mëposhtme për tangjenten dhe kotangjenten:

Rrethi trigonometrik
Grafikisht, marrëdhënia ndërmjet sasive të përmendura mund të paraqitet si më poshtë:

Rrethi, në këtë rast, përfaqëson të gjitha vlerat e mundshme të këndit α - nga 0° deri në 360°. Siç shihet nga figura, çdo funksion merr një vlerë negative ose pozitive në varësi të këndit. Për shembull, sin α do të ketë një shenjë "+" nëse α i përket çerekut 1 dhe 2 të rrethit, domethënë është në intervalin nga 0° deri në 180°. Për α nga 180° deri në 360° (tremujori III dhe IV), sin α mund të jetë vetëm një vlerë negative.
Le të përpiqemi të ndërtojmë tabela trigonometrike për kënde specifike dhe të zbulojmë kuptimin e sasive.

Vlerat e α të barabarta me 30°, 45°, 60°, 90°, 180° e kështu me radhë quhen raste të veçanta. Vlerat e funksioneve trigonometrike për to llogariten dhe paraqiten në formën e tabelave të veçanta.

Këto kënde nuk janë zgjedhur rastësisht. Emërtimi π në tabela është për radianët. Rad është këndi në të cilin gjatësia e harkut të rrethit korrespondon me rrezen e tij. Kjo vlerë u prezantua për të krijuar një varësi universale; kur llogaritet në radianë, gjatësia aktuale e rrezes në cm nuk ka rëndësi.

Këndet në tabela për funksionet trigonometrike korrespondojnë me vlerat e radianit:

Pra, nuk është e vështirë të merret me mend se 2π është një rreth i plotë ose 360°.
Vetitë e funksioneve trigonometrike: sinus dhe kosinus
Për të shqyrtuar dhe krahasuar vetitë themelore të sinusit dhe kosinusit, tangjentës dhe kotangjentit, është e nevojshme të vizatohen funksionet e tyre. Kjo mund të bëhet në formën e një kurbë të vendosur në një sistem koordinativ dy-dimensional.
Konsideroni tabelën krahasuese të vetive për sinusin dhe kosinusin:

| Vala sinusale | Kosinusi |
|---|---|
| y = sinx | y = cos x |
| ODZ [-1; 1] | ODZ [-1; 1] |
| sin x = 0, për x = πk, ku k ϵ Z | cos x = 0, për x = π/2 + πk, ku k ϵ Z |
| sin x = 1, për x = π/2 + 2πk, ku k ε Z | cos x = 1, në x = 2πk, ku k ε Z |
| sin x = - 1, në x = 3π/2 + 2πk, ku k ε Z | cos x = - 1, për x = π + 2πk, ku k ε Z |
| sin (-x) = - sin x, pra funksioni është tek | cos (-x) = cos x, pra funksioni është çift |
| funksioni është periodik, periudha më e vogël është 2π | |
| sin x › 0, me x që i përket çerekut 1 dhe 2 ose nga 0° deri në 180° (2πk, π + 2πk) | cos x › 0, me x që i përket lagjeve I dhe IV ose nga 270° në 90° (- π/2 + 2πk, π/2 + 2πk) |
| sin x ‹ 0, me x që i përket tremujorit të tretë dhe të katërt ose nga 180° në 360° (π + 2πk, 2π + 2πk) | cos x ‹ 0, me x që i përket tremujorit të dytë dhe të tretë ose nga 90° në 270° (π/2 + 2πk, 3π/2 + 2πk) |
| rritet në intervalin [- π/2 + 2πk, π/2 + 2πk] | rritet në intervalin [-π + 2πk, 2πk] |
| zvogëlohet në intervale [π/2 + 2πk, 3π/2 + 2πk] | zvogëlohet në intervale |
| derivat (sin x)’ = cos x | derivat (cos x)’ = - sin x |
Përcaktimi nëse një funksion është i barabartë apo jo është shumë i thjeshtë. Mjafton të imagjinoni një rreth trigonometrik me shenjat e sasive trigonometrike dhe të "palosni" mendërisht grafikun në lidhje me boshtin OX. Nëse shenjat përkojnë, funksioni është çift, përndryshe është tek.

Futja e radianeve dhe renditja e vetive themelore të valëve sinus dhe kosinus na lejojnë të paraqesim modelin e mëposhtëm:

Është shumë e lehtë të verifikosh nëse formula është e saktë. Për shembull, për x = π/2, sinusi është 1, siç është kosinusi i x = 0. Kontrolli mund të bëhet duke konsultuar tabelat ose duke gjurmuar kurbat e funksionit për vlerat e dhëna.
Vetitë e tangjentoideve dhe kotangjentoideve
Grafikët e funksioneve tangjente dhe kotangjente ndryshojnë ndjeshëm nga funksionet sinus dhe kosinus. Vlerat tg dhe ctg janë reciproke të njëra-tjetrës.


- Y = tan x.
- Tangjentja tenton te vlerat e y në x = π/2 + πk, por nuk i arrin kurrë ato.
- Periudha pozitive më e vogël e tangentoidit është π.
- Tg (- x) = - tg x, pra funksioni është tek.
- Tg x = 0, për x = πk.
- Funksioni po rritet.
- Tg x › 0, për x ε (πk, π/2 + πk).
- Tg x ‹ 0, për x ϵ (— π/2 + πk, πk).
- Derivati (tg x)' = 1/cos 2 x.
Merrni parasysh imazhin grafik të kotangjentoidit më poshtë në tekst.

Karakteristikat kryesore të kotangjentoideve:
- Y = ahur x.
- Ndryshe nga funksionet e sinusit dhe kosinusit, në tangentoidin Y mund të marrë vlerat e grupit të të gjithë numrave realë.
- Kotangjentoidi tenton në vlerat e y në x = πk, por kurrë nuk i arrin ato.
- Periudha më e vogël pozitive e një kotangjentoide është π.
- Ctg (- x) = - ctg x, pra funksioni është tek.
- Ctg x = 0, për x = π/2 + πk.
- Funksioni është në rënie.
- Ctg x › 0, për x ε (πk, π/2 + πk).
- Ctg x ‹ 0, për x ϵ (π/2 + πk, πk).
- Derivati (ctg x)’ = - 1/sin 2 x Saktë
Le të themi se Akili vrapon dhjetë herë më shpejt se breshka dhe është një mijë hapa pas saj. Gjatë kohës që i duhet Akilit për të vrapuar këtë distancë, breshka do të zvarritet njëqind hapa në të njëjtin drejtim. Kur Akili vrapon njëqind hapa, breshka zvarritet edhe dhjetë hapa të tjerë, e kështu me radhë. Procesi do të vazhdojë deri në pafundësi, Akili nuk do ta arrijë kurrë breshkën.
Ky arsyetim u bë një tronditje logjike për të gjithë brezat pasardhës. Aristoteli, Diogjeni, Kanti, Hegeli, Hilberti... Të gjithë e konsideronin aporinë e Zenonit në një mënyrë apo në një tjetër. Goditja ishte aq e fortë sa " ... diskutimet vazhdojnë edhe sot e kësaj dite; komuniteti shkencor nuk ka qenë ende në gjendje të arrijë në një mendim të përbashkët për thelbin e paradokseve ... analiza matematikore, teoria e grupeve, qasje të reja fizike dhe filozofike u përfshinë në studimin e çështjes ; asnjëri prej tyre nuk u bë një zgjidhje e pranuar përgjithësisht e problemit..."[Wikipedia, "Aporia e Zenos". Të gjithë e kuptojnë se po mashtrohen, por askush nuk e kupton se në çfarë konsiston mashtrimi.
Nga pikëpamja matematikore, Zeno në aporinë e tij tregoi qartë kalimin nga sasia në . Ky kalim nënkupton aplikim në vend të atyre të përhershëm. Me sa kuptoj unë, aparati matematikor për përdorimin e njësive të ndryshueshme të matjes ose nuk është zhvilluar ende, ose nuk është aplikuar në aporinë e Zenos. Zbatimi i logjikës sonë të zakonshme na çon në një kurth. Ne, për shkak të inercisë së të menduarit, aplikojmë njësi konstante të kohës në vlerën reciproke. Nga pikëpamja fizike, kjo duket sikur koha po ngadalësohet derisa të ndalojë plotësisht në momentin kur Akili kap breshkën. Nëse koha ndalon, Akili nuk mund ta kalojë më breshkën.
Nëse e kthejmë logjikën tonë të zakonshme, gjithçka bie në vend. Akili vrapon me një shpejtësi konstante. Çdo segment pasues i rrugës së tij është dhjetë herë më i shkurtër se ai i mëparshmi. Prandaj, koha e shpenzuar për tejkalimin e saj është dhjetë herë më pak se ajo e mëparshme. Nëse zbatojmë konceptin e "pafundësisë" në këtë situatë, atëherë do të ishte e saktë të thuhet "Akili do ta arrijë breshkën pafundësisht shpejt".
Si ta shmangni këtë kurth logjik? Qëndroni në njësi konstante kohore dhe mos kaloni në njësi reciproke. Në gjuhën e Zenonit duket kështu:
Në kohën që i duhen Akilit për të bërë një mijë hapa, breshka do të zvarritet njëqind hapa në të njëjtin drejtim. Gjatë intervalit tjetër kohor të barabartë me të parin, Akili do të vrapojë një mijë hapa të tjerë, dhe breshka do të zvarritet njëqind hapa. Tani Akili është tetëqind hapa përpara breshkës.
Kjo qasje përshkruan në mënyrë adekuate realitetin pa asnjë paradoks logjik. Por kjo nuk është një zgjidhje e plotë për problemin. Deklarata e Ajnshtajnit për papërmbajtshmërinë e shpejtësisë së dritës është shumë e ngjashme me aporinë e Zenonit "Akili dhe Breshka". Ne ende duhet të studiojmë, rimendojmë dhe zgjidhim këtë problem. Dhe zgjidhja duhet kërkuar jo në numër pafundësisht të madh, por në njësi matëse.
Një tjetër aporia interesante e Zenos tregon për një shigjetë fluturuese:
Një shigjetë fluturuese është e palëvizshme, pasi në çdo moment të kohës është në pushim, dhe duke qenë se është në pushim në çdo moment të kohës, ajo është gjithmonë në pushim.
Në këtë apori, paradoksi logjik kapërcehet shumë thjesht - mjafton të sqarohet se në çdo moment të kohës një shigjetë fluturuese është në pushim në pika të ndryshme të hapësirës, që në fakt është lëvizje. Këtu duhet theksuar edhe një pikë tjetër. Nga një fotografi e një makine në rrugë është e pamundur të përcaktohet as fakti i lëvizjes së saj, as distanca deri në të. Për të përcaktuar nëse një makinë po lëviz, ju nevojiten dy fotografi të bëra nga e njëjta pikë në pika të ndryshme kohore, por nuk mund të përcaktoni distancën prej tyre. Për të përcaktuar distancën nga një makinë, ju nevojiten dy fotografi të marra nga pika të ndryshme të hapësirës në një moment në kohë, por prej tyre nuk mund të përcaktoni faktin e lëvizjes (natyrisht, ju duhen ende të dhëna shtesë për llogaritjet, trigonometria do t'ju ndihmojë ). Ajo që dua të tërheq vëmendjen e veçantë është se dy pika në kohë dhe dy pika në hapësirë janë gjëra të ndryshme që nuk duhen ngatërruar, sepse ofrojnë mundësi të ndryshme për kërkime.
E mërkurë, 4 korrik 2018
Dallimet midis setit dhe multisetit përshkruhen shumë mirë në Wikipedia. Le të shohim.
Siç mund ta shihni, "nuk mund të ketë dy elementë identikë në një grup", por nëse ka elementë identikë në një grup, një grup i tillë quhet "shumë grup". Qeniet e arsyeshme nuk do ta kuptojnë kurrë një logjikë të tillë absurde. Ky është niveli i papagajve që flasin dhe majmunëve të stërvitur, të cilët nuk kanë inteligjencë nga fjala "plotësisht". Matematikanët veprojnë si trajnerë të zakonshëm, duke na predikuar idetë e tyre absurde.
Njëherë e një kohë, inxhinierët që ndërtuan urën ishin në një varkë nën urë ndërsa testonin urën. Nëse ura u shemb, inxhinieri mediokër vdiq nën rrënojat e krijimit të tij. Nëse ura mund të përballonte ngarkesën, inxhinieri i talentuar ndërtoi ura të tjera.
Pavarësisht se sa matematikanët fshihen pas shprehjes "mendoni mua, unë jam në shtëpi", ose më mirë, "matematika studion koncepte abstrakte", ekziston një kordon kërthizor që i lidh ato në mënyrë të pandashme me realitetin. Ky kordon kërthizor është para. Le të zbatojmë teorinë e grupeve matematikore për vetë matematikanët.
Ne kemi studiuar shumë mirë matematikën dhe tani jemi ulur në arkë, duke dhënë rroga. Pra, një matematikan vjen tek ne për paratë e tij. I numërojmë të gjithë shumën dhe e shtrojmë në tryezën tonë në pirgje të ndryshme, në të cilat vendosim fatura të së njëjtës emërtim. Pastaj marrim një faturë nga çdo grumbull dhe i japim matematikanit "pagën e tij matematikore". Le t'i shpjegojmë matematikanit se ai do të marrë faturat e mbetura vetëm kur të provojë se një grup pa elementë identikë nuk është i barabartë me një grup me elementë identikë. Këtu fillon argëtimi.
Para së gjithash, logjika e deputetëve do të funksionojë: "Kjo mund të zbatohet për të tjerët, por jo për mua!" Më pas ata do të fillojnë të na sigurojnë se faturat e të njëjtit emërtim kanë numra të ndryshëm faturash, që do të thotë se ato nuk mund të konsiderohen të njëjtat elementë. Mirë, le t'i numërojmë pagat në monedha - nuk ka numra në monedha. Këtu matematikani do të fillojë të kujtojë furishëm fizikën: monedha të ndryshme kanë sasi të ndryshme papastërtie, struktura kristalore dhe renditja e atomeve është unike për secilën monedhë...
Dhe tani kam pyetjen më interesante: ku është vija përtej së cilës elementët e një grupi të shumëfishtë kthehen në elementë të një grupi dhe anasjelltas? Një linjë e tillë nuk ekziston - gjithçka vendoset nga shamanët, shkenca nuk është as afër të gënjejë këtu.
Shikoni këtu. Ne zgjedhim stadiume futbolli me të njëjtën zonë. Zonat e fushave janë të njëjta - që do të thotë se ne kemi një shumë grup. Por po të shikojmë emrat e po këtyre stadiumeve, marrim shumë, sepse emrat janë të ndryshëm. Siç mund ta shihni, i njëjti grup elementësh është një grup dhe një grup shumëfish. Cila është e saktë? Dhe këtu matematikani-shaman-sharpist nxjerr nga mëngët një ace atuesh dhe fillon të na tregojë ose për një grup ose një multiset. Në çdo rast, ai do të na bindë se ka të drejtë.
Për të kuptuar se si shamanët modernë veprojnë me teorinë e grupeve, duke e lidhur atë me realitetin, mjafton t'i përgjigjemi një pyetjeje: si ndryshojnë elementët e një grupi nga elementët e një grupi tjetër? Unë do t'ju tregoj, pa asnjë "të konceptueshme si jo një tërësi e vetme" ose "jo e konceptueshme si një tërësi e vetme".
e diel, 18 mars 2018
Shuma e shifrave të një numri është një valle e shamanëve me një dajre, e cila nuk ka të bëjë fare me matematikën. Po, në mësimet e matematikës ne jemi mësuar të gjejmë shumën e shifrave të një numri dhe ta përdorim atë, por kjo është arsyeja pse ata janë shamanë, për t'u mësuar pasardhësve të tyre aftësitë dhe mençurinë e tyre, përndryshe shamanët thjesht do të vdesin.
Keni nevojë për prova? Hapni Wikipedia dhe provoni të gjeni faqen "Shuma e shifrave të një numri". Ajo nuk ekziston. Nuk ka asnjë formulë në matematikë që mund të përdoret për të gjetur shumën e shifrave të çdo numri. Në fund të fundit, numrat janë simbole grafike me të cilat ne shkruajmë numra, dhe në gjuhën e matematikës detyra tingëllon kështu: "Gjeni shumën e simboleve grafike që përfaqësojnë çdo numër". Matematikanët nuk mund ta zgjidhin këtë problem, por shamanët mund ta bëjnë atë lehtësisht.
Le të kuptojmë se çfarë dhe si bëjmë për të gjetur shumën e shifrave të një numri të caktuar. Dhe kështu, le të kemi numrin 12345. Çfarë duhet bërë për të gjetur shumën e shifrave të këtij numri? Le të shqyrtojmë të gjitha hapat në rend.
1. Shkruani numrin në një copë letër. Çfarë kemi bërë? Ne e kemi kthyer numrin në një simbol grafik numerik. Ky nuk është një operacion matematikor.
2. Ne e premë një fotografi që rezulton në disa fotografi që përmbajnë numra individualë. Prerja e një fotografie nuk është një operacion matematikor.
3. Shndërroni simbolet individuale grafike në numra. Ky nuk është një operacion matematikor.
4. Shtoni numrat që rezultojnë. Tani kjo është matematika.
Shuma e shifrave të numrit 12345 është 15. Këto janë "kurset e prerjes dhe qepjes" të mësuara nga shamanët që përdorin matematikanët. Por kjo nuk është e gjitha.
Nga pikëpamja matematikore, nuk ka rëndësi se në cilin sistem numrash shkruajmë një numër. Pra, në sisteme të ndryshme numrash shuma e shifrave të të njëjtit numër do të jetë e ndryshme. Në matematikë, sistemi i numrave tregohet si nënshkrim në të djathtë të numrit. Me numrin e madh 12345, nuk dua të mashtroj kokën, le të marrim parasysh numrin 26 nga artikulli rreth. Le ta shkruajmë këtë numër në sistemet e numrave binar, oktal, dhjetor dhe heksadecimal. Ne nuk do të shikojmë çdo hap nën një mikroskop; ne e kemi bërë tashmë këtë. Le të shohim rezultatin.
Siç mund ta shihni, në sisteme të ndryshme numrash shuma e shifrave të të njëjtit numër është e ndryshme. Ky rezultat nuk ka të bëjë fare me matematikën. Është njësoj sikur të përcaktoni sipërfaqen e një drejtkëndëshi në metra dhe centimetra, do të merrnit rezultate krejtësisht të ndryshme.
Zero duket e njëjtë në të gjitha sistemet e numrave dhe nuk ka shumë shifrash. Ky është një argument tjetër në favor të faktit se. Pyetje për matematikanët: si përcaktohet diçka që nuk është numër në matematikë? Çfarë, për matematikanët nuk ekziston asgjë përveç numrave? Unë mund ta lejoj këtë për shamanët, por jo për shkencëtarët. Realiteti nuk ka të bëjë vetëm me numrat.
Rezultati i marrë duhet të konsiderohet si provë se sistemet e numrave janë njësi matëse për numrat. Në fund të fundit, ne nuk mund të krahasojmë numrat me njësi të ndryshme matëse. Nëse të njëjtat veprime me njësi të ndryshme matëse të së njëjtës sasi çojnë në rezultate të ndryshme pas krahasimit të tyre, atëherë kjo nuk ka të bëjë fare me matematikën.
Çfarë është matematika e vërtetë? Kjo ndodh kur rezultati i një operacioni matematikor nuk varet nga madhësia e numrit, njësia matëse e përdorur dhe nga kush e kryen këtë veprim.
Oh! A nuk është ky banja e grave?
- Grua e re! Ky është një laborator për studimin e shenjtërisë indefilike të shpirtrave gjatë ngjitjes së tyre në qiell! Halo në krye dhe shigjeta lart. Çfarë tualeti tjetër?
Femër... Halo sipër dhe shigjeta poshtë janë mashkull.
Nëse një vepër e tillë e artit të dizajnit shkëlqen para syve tuaj disa herë në ditë,
Atëherë nuk është për t'u habitur që papritmas gjeni një ikonë të çuditshme në makinën tuaj:
Personalisht, unë përpiqem të shoh minus katër gradë në një person që po dergjet (një foto) (një përbërje prej disa fotografish: një shenjë minus, numri katër, një përcaktim shkallësh). Dhe nuk mendoj se kjo vajzë është një budallaqe që nuk di fizikë. Ajo thjesht ka një stereotip të fortë të perceptimit të imazheve grafike. Dhe matematikanët na mësojnë këtë gjatë gjithë kohës. Ja një shembull.
1A nuk është "minus katër gradë" ose "një a". Ky është "njeriu i kulluar" ose numri "njëzet e gjashtë" në shënimin heksadecimal. Ata njerëz që vazhdimisht punojnë në këtë sistem numrash e perceptojnë automatikisht një numër dhe një shkronjë si një simbol grafik.
Tabela e vlerave të funksioneve trigonometrike
shënim. Kjo tabelë e vlerave të funksionit trigonometrik përdor shenjën √ për të përfaqësuar rrënjën katrore. Për të treguar një fraksion, përdorni simbolin "/".
Shiko gjithashtu materiale të dobishme:
Për përcaktimi i vlerës së një funksioni trigonometrik, gjeni atë në kryqëzimin e drejtëzës që tregon funksionin trigonometrik. Për shembull, sinusi 30 gradë - ne kërkojmë kolonën me titullin sin (sinus) dhe gjejmë kryqëzimin e kësaj kolone tabele me rreshtin "30 gradë", në kryqëzimin e tyre lexojmë rezultatin - një gjysmë. Në mënyrë të ngjashme ne gjejmë kosinusi 60 gradë, sinusi 60 gradë (edhe një herë, në kryqëzimin e kolonës sin dhe vijës 60 gradë gjejmë vlerën sin 60 = √3/2), etj. Vlerat e sinuseve, kosinuseve dhe tangjentëve të këndeve të tjera "popullore" gjenden në të njëjtën mënyrë.
Sinus pi, kosinus pi, tangjente pi dhe kënde të tjera në radiane
Tabela e mëposhtme e kosinuseve, sinuseve dhe tangjenteve është gjithashtu e përshtatshme për të gjetur vlerën e funksioneve trigonometrike, argumenti i të cilëve është dhënë në radianë. Për ta bërë këtë, përdorni kolonën e dytë të vlerave të këndit. Falë kësaj, ju mund të konvertoni vlerën e këndeve popullore nga gradë në radiane. Për shembull, le të gjejmë këndin 60 gradë në rreshtin e parë dhe të lexojmë vlerën e tij në radianë nën të. 60 gradë është e barabartë me π/3 radian.
Numri pi shpreh në mënyrë të paqartë varësinë e perimetrit nga masa e shkallës së këndit. Kështu, radianët pi janë të barabartë me 180 gradë.
Çdo numër i shprehur në terma pi (radianët) mund të shndërrohet lehtësisht në gradë duke zëvendësuar pi (π) me 180.
Shembuj:
1. Sine pi.
sin π = mëkat 180 = 0
pra, sinusi i pi është i njëjtë me sinusin 180 gradë dhe është i barabartë me zero.
2. Kosinusi pi.
cos π = cos 180 = -1
pra, kosinusi i pi është i njëjtë me kosinusin 180 gradë dhe është i barabartë me minus një.
3. Tangjenta pi
tg π = tg 180 = 0
pra, tangjentja pi është e njëjtë me tangjenten 180 gradë dhe është e barabartë me zero.
Tabela e vlerave të sinusit, kosinusit, tangjentes për këndet 0 - 360 gradë (vlerat e zakonshme)
|
vlera e këndit α (gradë) |
vlera e këndit α (përmes pi) |
mëkat (sinus) |
cos (kosinus) |
tg (tangjente) |
ctg (kotangjente) |
sek (sekent) |
cosec (bashkërenditëse) |
| 0 | 0 | 0 | 1 | 0 | - | 1 | - |
| 15 | π/12 | 2 - √3 | 2 + √3 | ||||
| 30 | π/6 | 1/2 | √3/2 | 1/√3 | √3 | 2/√3 | 2 |
| 45 | π/4 | √2/2 | √2/2 | 1 | 1 | √2 | √2 |
| 60 | π/3 | √3/2 | 1/2 | √3 | 1/√3 | 2 | 2/√3 |
| 75 | 5π/12 | 2 + √3 | 2 - √3 | ||||
| 90 | π/2 | 1 | 0 | - | 0 | - | 1 |
| 105 | 7π/12 |
- |
- 2 - √3 | √3 - 2 | |||
| 120 | 2π/3 | √3/2 | -1/2 | -√3 | -√3/3 | ||
| 135 | 3π/4 | √2/2 | -√2/2 | -1 | -1 | -√2 | √2 |
| 150 | 5π/6 | 1/2 | -√3/2 | -√3/3 | -√3 | ||
| 180 | π | 0 | -1 | 0 | - | -1 | - |
| 210 | 7π/6 | -1/2 | -√3/2 | √3/3 | √3 | ||
| 240 | 4π/3 | -√3/2 | -1/2 | √3 | √3/3 | ||
| 270 | 3π/2 | -1 | 0 | - | 0 | - | -1 |
| 360 | 2π | 0 | 1 | 0 | - | 1 | - |
Nëse në tabelën e vlerave të funksioneve trigonometrike tregohet një vizë në vend të vlerës së funksionit (tangjente (tg) 90 gradë, kotangjente (ctg) 180 gradë), atëherë për një vlerë të caktuar të masës së shkallës së këndit funksioni nuk ka një vlerë specifike. Nëse nuk ka vizë, qeliza është bosh, që do të thotë se nuk e kemi futur ende vlerën e kërkuar. Ne jemi të interesuar se për çfarë pyetjesh na vijnë përdoruesit dhe plotësojnë tabelën me vlera të reja, pavarësisht nga fakti se të dhënat aktuale për vlerat e kosinuseve, sinuseve dhe tangjenteve të vlerave më të zakonshme të këndit janë mjaft të mjaftueshme për të zgjidhur shumicën problemet.
Tabela e vlerave të funksioneve trigonometrike sin, cos, tg për këndet më të njohura
0, 15, 30, 45, 60, 90 ... 360 gradë
(vlerat numerike "sipas tabelave Bradis")
| vlera e këndit α (gradë) | vlera e këndit α në radiane | mëkat (sinus) | cos (kosinus) | tg (tangjente) | ctg (kotangjent) |
|---|---|---|---|---|---|
| 0 | 0 | ||||
| 15 |
0,2588 |
0,9659
|
0,2679 |
||
| 30 |
0,5000 |
0,5774 |
|||
| 45 |
0,7071 |
||||
|
0,7660 |
|||||
| 60 |
0,8660 |
0,5000
|
1,7321 |
||
|
7π/18 |
E përqendruar në një pikë A.
α
- këndi i shprehur në radianë.
Përkufizimi
Sinus (sin α)është një funksion trigonometrik në varësi të këndit α ndërmjet hipotenuzës dhe këmbës së një trekëndëshi kënddrejtë, i barabartë me raportin e gjatësisë së këmbës së kundërt |BC| në gjatësinë e hipotenuzës |AC|.
Kosinusi (cos α)është një funksion trigonometrik në varësi të këndit α ndërmjet hipotenuzës dhe këmbës së një trekëndëshi kënddrejtë, i barabartë me raportin e gjatësisë së këmbës ngjitur |AB| në gjatësinë e hipotenuzës |AC|.
Shënime të pranuara
;
;
.
;
;
.
Grafiku i funksionit sinus, y = sin x
Grafiku i funksionit të kosinusit, y = cos x

Vetitë e sinusit dhe kosinusit
Periodiciteti
Funksionet y = mëkat x dhe y = cos x periodike me perioda 2π.
Barazi
Funksioni i sinusit është tek. Funksioni kosinus është i barabartë.
Domeni i përkufizimit dhe vlerave, ekstreme, rritje, ulje
Funksionet e sinusit dhe kosinusit janë të vazhdueshme në domenin e tyre të përkufizimit, domethënë për të gjitha x (shih vërtetimin e vazhdimësisë). Vetitë e tyre kryesore janë paraqitur në tabelë (n - numër i plotë).
| y = mëkat x | y = cos x | |
| Shtrirja dhe vazhdimësia | - ∞ < x < + ∞ | - ∞ < x < + ∞ |
| Gama e vlerave | -1 ≤ y ≤ 1 | -1 ≤ y ≤ 1 |
| Në rritje | ||
| Duke zbritur | ||
| Maksima, y = 1 | ||
| Minimum, y = - 1 | ||
| Zero, y = 0 | ||
| Pikat e prerjes me boshtin e ordinatave, x = 0 | y = 0 | y = 1 |
Formulat bazë
Shuma e katrorëve të sinusit dhe kosinusit
Formulat për sinusin dhe kosinusin nga shuma dhe diferenca
;
;
Formulat për prodhimin e sinuseve dhe kosinuseve
Formulat e shumës dhe diferencës
Shprehja e sinusit përmes kosinusit
;
;
;
.
Shprehja e kosinusit përmes sinusit
;
;
;
.
Shprehja përmes tangjentes
; .
Kur , kemi:
;
.
Në:
;
.
Tabela e sinuseve dhe kosinuseve, tangjentëve dhe kotangjenteve
Kjo tabelë tregon vlerat e sinuseve dhe kosinuseve për vlera të caktuara të argumentit. 
Shprehjet përmes ndryshoreve komplekse
;
formula e Euler-it
Shprehjet përmes funksioneve hiperbolike
;
;
Derivatet
; . Nxjerrja e formulave > > >
Derivatet e rendit të n-të:
{ -∞ <
x < +∞ }
Secant, kosekant
Funksionet e anasjellta
Funksionet e anasjellta të sinusit dhe kosinusit janë përkatësisht arksina dhe arkozina.
Arcsine, arcsin
Arccosine, arccos
Referencat:
NË. Bronstein, K.A. Semendyaev, Manual i matematikës për inxhinierë dhe studentë të kolegjit, "Lan", 2009.