Rzuty prędkości i przyspieszenia. Prędkość ruchu Moduł rzutowania prędkości na oś x

Rzuty prędkości dwóch punktów ciała sztywnego na oś przechodzącą przez te punkty są sobie równe.
w A cos α = v B cos β.

Dowód

Wybierzmy prostokątny stały układ współrzędnych Oxyz. Weźmy dwa dowolne punkty ciała sztywnego A i B. Pozwalać (x A , y A , z A ) I (x B , y B , z B )- współrzędne tych punktów. Kiedy ciało sztywne się porusza, są to funkcje czasu t. Różniczkując ze względu na czas otrzymujemy rzuty prędkości punktów.
, .

Skorzystajmy z faktu, że gdy porusza się ciało sztywne, odległość | AB| pomiędzy punktami pozostaje stała, to znaczy nie zależy od czasu t. Stały jest również kwadrat odległości
.
Zróżniczkujmy to równanie ze względu na czas t, stosując zasadę różniczkowania funkcji zespolonej.

Skróćmy to 2 .
(1)

Przedstawmy wektor
.
Następnie równanie (1) można przedstawić jako iloczyn skalarny wektorów.
(2)
Przeprowadzamy transformacje.
;
(3) .
Według właściwości iloczynu skalarnego
,
.
Zastąp w (3) i zmniejsz o | AB|.
;

co było do okazania

Prędkość względna

Rozważmy ruch punktu B względem punktu A. Wprowadźmy prędkość względną punktu B względem A.

Następnie równanie (2) można przepisać w postaci
.

Oznacza to, że prędkość względna jest prostopadła do wektora narysowanego z punktu A do punktu B. Ponieważ punkt B jest brany arbitralnie, względna prędkość dowolnego punktu ciała sztywnego jest prostopadła do wektora promienia narysowanego z punktu A. Oznacza to, że względem punktu A ciało podlega ruchowi obrotowemu. Względną prędkość punktów ciała określa wzór na ruch obrotowy
.

Często nazywany jest punkt A, względem którego rozpatrywany jest ruch Polak.

Prędkość bezwzględną punktu B względem ustalonego układu współrzędnych można zapisać w postaci:
.
Jest równa sumie prędkości ruchu postępowego dowolnego punktu A (bieguna) i prędkości ruchu obrotowego względem bieguna A.

Przykład rozwiązania problemu

Zadanie

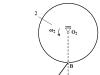
Koła 1 i 2 o promieniu R 1 = 0,15 m i R 2 = 0,3 m, odpowiednio, są połączone zawiasami z prętem o 3 długościach | AB| = 0,5 m. Koło 1 obraca się z prędkością kątową ω 1 = 1 rad/s. Dla położenia mechanizmu pokazanego na rysunku wyznacz prędkość kątową ω 2 koła 2. Weź L = 0,3 m.

Rozwiązanie problemu

Punkt A porusza się po okręgu promień r 1 wokół środka obrotu O 1 . Prędkość punktu A określa wzór
V A = ω 1 R 1.
Wektor jest skierowany pionowo (prostopadle do O 1 A).

Punkt B porusza się po okręgu promień r 2 wokół środka obrotu O 2 . Prędkość punktu B określa wzór
VB = ω 2 R 2.
Stąd
.
Wektor jest skierowany poziomo (prostopadle do O 2 B).

Budujemy trójkąt prostokątny ABC. Stosujemy twierdzenie Pitagorasa.
(M)
.
Cosinus kąta między wektorem prędkości a prostą AB w kierunku wektora jest równy
.

Przez twierdzenie o projekcji prędkości dwa punkty ciała sztywnego na prostej mamy:
V A cos α = V B cos β.
Stąd
.

Wyznaczanie prędkości kątowej koła 2.
rad/s.

Jednolity ruch– jest to ruch ze stałą prędkością, czyli gdy prędkość się nie zmienia (v = const) i nie następuje przyspieszanie lub zwalnianie (a = 0).

Ruch po linii prostej- jest to ruch po linii prostej, to znaczy trajektoria ruchu prostoliniowego jest linią prostą.

Jednolity ruch liniowy- jest to ruch, podczas którego ciało wykonuje równe ruchy w równych odstępach czasu. Przykładowo, jeśli podzielimy pewien przedział czasu na jednosekundowe odstępy, to przy ruchu jednostajnym ciało w każdym z tych odstępów czasu przebędzie tę samą odległość.

Prędkość jednostajnego ruchu prostoliniowego nie zależy od czasu i w każdym punkcie trajektorii jest skierowana w taki sam sposób, jak ruch ciała. Oznacza to, że wektor przemieszczenia pokrywa się w kierunku z wektorem prędkości. W tym przypadku prędkość średnia w dowolnym okresie czasu jest równa prędkości chwilowej: v cp = v Prędkość jednolitego ruchu prostoliniowego jest wielkością wektora fizycznego równą stosunkowi ruchu ciała w dowolnym okresie czasu do wartości tego przedziału t:

Zatem prędkość jednostajnego ruchu prostoliniowego pokazuje, ile ruchu wykonuje punkt materialny w jednostce czasu.

Poruszający przy jednostajnym ruchu liniowym określa się ze wzoru:

Przebyty dystans w ruchu liniowym jest równy modułowi przemieszczenia. Jeżeli dodatni kierunek osi OX pokrywa się z kierunkiem ruchu, to rzut prędkości na oś OX jest równy wielkości prędkości i jest dodatni:

V x = v, czyli v > 0 Rzut przemieszczenia na oś OX jest równy: s = vt = x – x 0 gdzie x 0 jest współrzędną początkową ciała, x jest współrzędną końcową ciała (lub współrzędna ciała w dowolnym momencie)

Równanie ruchu, czyli zależność współrzędnych ciała od czasu x = x(t), przyjmuje postać:

X = x 0 + vt Jeżeli dodatni kierunek osi OX jest przeciwny do kierunku ruchu ciała, to rzut prędkości ciała na oś OX jest ujemny, prędkość jest mniejsza od zera (v x = x 0 - wt

Zależność prędkości, współrzędnych i drogi od czasu

Zależność rzutu prędkości ciała od czasu pokazano na rys. 1.11. Ponieważ prędkość jest stała (v = const), wykres prędkości jest linią prostą równoległą do osi czasu Ot.

Ryż. 1.11. Zależność rzutu prędkości ciała od czasu dla ruchu jednostajnego prostoliniowego.

Rzut ruchu na oś współrzędnych jest liczbowo równy polu prostokąta OABC (ryc. 1.12), ponieważ wielkość wektora ruchu jest równa iloczynowi wektora prędkości i czasu, w którym ruch był zrobiony.

Ryż. 1.12. Zależność rzutu przemieszczenia ciała od czasu dla ruchu jednostajnego prostoliniowego.

Wykres przemieszczenia w funkcji czasu pokazano na ryc. 1.13. Wykres pokazuje, że rzut prędkości jest równy

V = s 1 / t 1 = tan α gdzie α jest kątem nachylenia wykresu do osi czasu. Im większy kąt α, tym szybciej porusza się ciało, to znaczy większa jest jego prędkość (im dłuższą drogę ciało pokonuje w krótszym czasie). Tangens stycznej do wykresu współrzędnych w funkcji czasu jest równa prędkości: tg α = v

Ryż. 1.13. Zależność rzutu przemieszczenia ciała od czasu dla ruchu jednostajnego prostoliniowego.

Zależność współrzędnej od czasu pokazano na ryc. 1.14. Z rysunku wynika, że

Tg α 1 > tan α 2 zatem prędkość ciała 1 jest większa od prędkości ciała 2 (v 1 > v 2). tg α 3 = v 3 Jeżeli ciało znajduje się w spoczynku, to wykres współrzędnych jest linią prostą równoległą do osi czasu, czyli x = x 0

Ryż. 1.14. Zależność współrzędnych ciała od czasu dla ruchu jednostajnego prostoliniowego.

Szybkość jest jedną z głównych cech. Wyraża samą istotę ruchu, tj. określa różnicę pomiędzy ciałem nieruchomym a ciałem poruszającym się.

Jednostką prędkości w układzie SI jest SM.

Należy pamiętać, że prędkość jest wielkością wektorową. Kierunek wektora prędkości jest wyznaczany przez ruch. Wektor prędkości jest zawsze skierowany stycznie do trajektorii w punkcie, przez który przechodzi poruszające się ciało (rys. 1).

Weźmy na przykład pod uwagę koło jadącego samochodu. Koło się obraca, a wszystkie punkty koła poruszają się po okręgach. Wylatujące z koła plamy będą lecieć stycznie do tych okręgów, wskazując kierunki wektorów prędkości poszczególnych punktów koła.

Zatem prędkość charakteryzuje kierunek ruchu ciała (kierunek wektora prędkości) i prędkość jego ruchu (moduł wektora prędkości).

Ujemna prędkość

Czy prędkość ciała może być ujemna? Tak, może. Jeżeli prędkość ciała jest ujemna, oznacza to, że ciało porusza się w kierunku przeciwnym do kierunku osi współrzędnych w wybranym układzie odniesienia. Rysunek 2 przedstawia ruch autobusu i samochodu osobowego. Prędkość samochodu jest ujemna, a prędkość autobusu dodatnia. Należy pamiętać, że mówiąc o znaku prędkości mamy na myśli rzut wektora prędkości na oś współrzędnych.

Ruch równomierny i nierówny

Ogólnie rzecz biorąc, prędkość zależy od czasu. W zależności od charakteru zależności prędkości od czasu, ruch może być równomierny lub nierówny.

DEFINICJA

Jednolity ruch– jest to ruch ze stałą prędkością modułu.

W przypadku nierównomiernego ruchu mówimy o:

Przykłady rozwiązywania problemów na temat „Prędkość”

PRZYKŁAD 1

Ćwiczenia	Samochód pierwszą połowę podróży pomiędzy dwiema osadami pokonał z prędkością 90 km/h, a drugą połowę z prędkością 54 km/h. Wyznacz średnią prędkość samochodu.
Rozwiązanie	Błędem byłoby obliczanie średniej prędkości samochodu jako średniej arytmetycznej dwóch wskazanych prędkości. Skorzystajmy z definicji prędkości średniej: Ponieważ zakłada się ruch jednostajny prostoliniowy, znaki wektorów można pominąć. Czas spędzony przez samochód na pokonaniu całego dystansu: gdzie to czas spędzony na ukończeniu pierwszej połowy ścieżki, a to czas spędzony na ukończeniu drugiej połowy ścieżki. Całkowity ruch jest równy odległości między obszarami zaludnionymi, tj. . Podstawiając te stosunki do wzoru na średnią prędkość, otrzymujemy: Przeliczmy prędkości na poszczególnych odcinkach na układ SI: Wtedy średnia prędkość samochodu wynosi: (SM)
Odpowiedź	Średnia prędkość samochodu wynosi 18,8 m/s

PRZYKŁAD 2

Ćwiczenia	Samochód jedzie przez 10 sekund z prędkością 10 m/s, a następnie przez kolejne 2 minuty jedzie z prędkością 25 m/s. Wyznacz średnią prędkość samochodu.
Rozwiązanie	Zróbmy rysunek.

3.1. Ruch jednostajny po linii prostej.

3.1.1. Ruch jednostajny po linii prostej- ruch po linii prostej ze stałą wartością i kierunkiem przyspieszenia:

3.1.2. Przyśpieszenie()- fizyczna wielkość wektora pokazująca, jak bardzo zmieni się prędkość w ciągu 1 s.

W formie wektorowej:

gdzie jest prędkością początkową ciała, jest prędkością ciała w chwili czasu T.

W rzucie na oś Wół:

gdzie jest rzutem prędkości początkowej na oś Wół, - rzut prędkości ciała na oś Wół w pewnym momencie T.

Znaki rzutów zależą od kierunku wektorów i osi Wół.

3.1.3. Wykres projekcyjny przyspieszenia w funkcji czasu.

Przy ruchu równomiernie naprzemiennym przyspieszenie jest stałe, dlatego będzie widoczne jako linie proste równoległe do osi czasu (patrz rysunek):

3.1.4. Prędkość podczas ruchu jednostajnego.

W formie wektorowej:

W rzucie na oś Wół:

Dla ruchu jednostajnie przyspieszonego:

Aby uzyskać jednolite zwolnione tempo:

3.1.5. Wykres projekcyjny prędkości w funkcji czasu.

Wykres rzutu prędkości w funkcji czasu jest linią prostą.

Kierunek ruchu: jeśli wykres (lub jego część) znajduje się powyżej osi czasu, wówczas ciało porusza się w dodatnim kierunku osi Wół.

Wartość przyspieszenia: im większa tangens kąta nachylenia (im bardziej stromo wznosi się lub opada), tym większy jest moduł przyspieszenia; gdzie jest zmiana prędkości w czasie

Przecięcie z osią czasu: jeżeli wykres przecina oś czasu, to przed punktem przecięcia ciało zwalniało (ruch równomiernie powolny), a po punkcie przecięcia zaczynało przyspieszać w przeciwnym kierunku (ruch równomiernie przyspieszany).

3.1.6. Znaczenie geometryczne pola pod wykresem w osiach

Obszar pod wykresem na osi Oj prędkość jest opóźniona i na osi Wół- czas to droga, którą przebywa ciało.

Na ryc. Rysunek 3.5 przedstawia przypadek ruchu jednostajnie przyspieszonego. Ścieżka w tym przypadku będzie równa powierzchni trapezu: (3.9)

3.1.7. Wzory obliczania ścieżki

Ruch równomiernie przyspieszony	Równe zwolnione tempo
(3.10)	(3.12)
(3.11)	(3.13)
(3.14)

Wszystkie wzory przedstawione w tabeli działają tylko przy zachowaniu kierunku ruchu, czyli do momentu przecięcia się prostej z osią czasu na wykresie rzutu prędkości w funkcji czasu.

Jeśli nastąpiło przecięcie, ruch łatwiej jest podzielić na dwa etapy:

przed przekroczeniem (hamowaniem):

Po skrzyżowaniu (przyspieszenie, ruch w przeciwnym kierunku)

We wzorach powyższych - czas od rozpoczęcia ruchu do przecięcia z osią czasu (czas przed zatrzymaniem), - droga, jaką przebyło ciało od początku ruchu do przecięcia z osią czasu, - czas, jaki upłynął od momentu przekroczenia osi czasu do chwili obecnej T, - droga, jaką przebyło ciało w przeciwnym kierunku w czasie, jaki upłynął od momentu przekroczenia osi czasu do tego momentu T, - moduł wektora przemieszczenia dla całego czasu ruchu, L- droga, którą przebyło ciało podczas całego ruchu.

3.1.8. Ruch w setnej sekundzie.

W tym czasie ciało przebędzie następującą drogę:

W tym czasie ciało przebędzie następującą drogę:

Następnie w tym przedziale ciało przebędzie następującą drogę:

Za przerwę można uznać dowolny okres czasu. Najczęściej z.

Następnie w ciągu 1 sekundy ciało pokonuje następującą drogę:

Za 2 sekundy:

Za 3 sekundy:

Jeśli przyjrzymy się uważnie, zobaczymy to itp.

W ten sposób dochodzimy do wzoru:

Słowem: drogi, jakie przebywa ciało w kolejnych okresach czasu, powiązane są ze sobą ciągiem liczb nieparzystych, a to nie zależy od przyspieszenia, z jakim porusza się ciało. Podkreślamy, że ta relacja obowiązuje dla

3.1.9. Równanie współrzędnych ciała dla ruchu jednostajnego

Równanie współrzędnych

Znaki rzutów prędkości początkowej i przyspieszenia zależą od względnego położenia odpowiednich wektorów i osi Wół.

Aby rozwiązać problemy, należy do równania dodać równanie na zmianę rzutu prędkości na oś:

3.2. Wykresy wielkości kinematycznych dla ruchu prostoliniowego

3.3. Ciało swobodnego spadania

Przez spadek swobodny rozumiemy następujący model fizyczny:

1) Upadek następuje pod wpływem grawitacji:

2) Nie ma oporu powietrza (w problemach czasami piszą „pomiń opór powietrza”);

3) Wszystkie ciała, niezależnie od masy, spadają z tym samym przyspieszeniem (czasami dodają „niezależnie od kształtu ciała”, ale bierzemy pod uwagę ruch tylko punktu materialnego, więc kształt ciała nie jest już brany pod uwagę na konto);

4) Przyspieszenie ziemskie jest skierowane ściśle w dół i na powierzchni Ziemi jest równe (w zadaniach, które często przyjmujemy dla wygody obliczeń);

3.3.1. Równania ruchu w rzucie na oś Oj

W odróżnieniu od ruchu po poziomej linii prostej, gdy nie wszystkie zadania wiążą się ze zmianą kierunku ruchu, przy swobodnym spadku najlepiej od razu skorzystać z równań zapisanych w rzutach na oś Oj.

Równanie współrzędnych ciała:

Równanie projekcji prędkości:

Z reguły w przypadku problemów wygodnie jest wybrać oś Oj w następujący sposób:

Oś Oj skierowany pionowo w górę;

Początek pokrywa się z poziomem Ziemi lub najniższym punktem trajektorii.

Przy takim wyborze równania i zostaną przepisane w następującej postaci:

3.4. Ruch w płaszczyźnie Oksy.

Rozważaliśmy ruch ciała z przyspieszeniem po linii prostej. Jednak ruch jednostajnie zmienny nie ogranicza się do tego. Na przykład ciało rzucone pod kątem do poziomu. W takich problemach należy wziąć pod uwagę ruch wzdłuż dwóch osi jednocześnie:

Lub w formie wektorowej:

Oraz zmiana rzutu prędkości na obie osie:

3.5. Zastosowanie pojęcia pochodnej i całki

Nie będziemy tutaj podawać szczegółowej definicji pochodnej i całki. Do rozwiązywania problemów potrzebujemy jedynie małego zestawu formuł.

Pochodna:

Gdzie A, B i to jest wartości stałe.

Całka:

Zobaczmy teraz, jak pojęcia pochodnej i całki odnoszą się do wielkości fizycznych. W matematyce pochodną oznacza się przez „”, w fizyce pochodną po czasie oznacza się przez „∙” nad funkcją.

Prędkość:

oznacza to, że prędkość jest pochodną wektora promienia.

Dla projekcji prędkości:

Przyśpieszenie:

to znaczy przyspieszenie jest pochodną prędkości.

Dla projekcji przyspieszenia:

Znając zatem prawo ruchu, łatwo możemy znaleźć zarówno prędkość, jak i przyspieszenie ciała.

Skorzystajmy teraz z pojęcia całki.

Prędkość:

oznacza to, że prędkość można znaleźć jako całkę przyspieszenia po czasie.

Wektor promienia:

to znaczy wektor promienia można znaleźć, całkując funkcję prędkości.

Znając zatem funkcję, możemy łatwo znaleźć zarówno prędkość, jak i prawo ruchu ciała.

Stałe we wzorach wyznacza się z warunków początkowych – wartości i chwili czasu

3.6. Trójkąt prędkości i trójkąt przemieszczenia

3.6.1. Trójkąt prędkości

W postaci wektorowej przy stałym przyspieszeniu prawo zmiany prędkości ma postać (3.5):

Wzór ten oznacza, że ​​wektor jest równy sumie wektorów i sumę wektorów można zawsze przedstawić na rysunku (patrz rysunek).

W każdym zadaniu, w zależności od warunków, trójkąt prędkości będzie miał swoją własną postać. Taka reprezentacja pozwala na wykorzystanie w rozwiązaniu rozważań geometrycznych, co często upraszcza rozwiązanie problemu.

3.6.2. Trójkąt ruchów

W postaci wektorowej zasada ruchu ze stałym przyspieszeniem ma postać:

Rozwiązując zadanie, można wybrać układ odniesienia w najwygodniejszy sposób, zatem nie tracąc na ogólności, możemy wybrać układ odniesienia w taki sposób, że początek układu współrzędnych umieścimy w punkcie, w którym ciało znajduje się w chwili początkowej. Następnie

to znaczy wektor jest równy sumie wektorów i przedstawmy to na rysunku (patrz rysunek).

Podobnie jak w poprzednim przypadku, w zależności od warunków, trójkąt przemieszczenia będzie miał swój własny kształt. Taka reprezentacja pozwala na wykorzystanie w rozwiązaniu rozważań geometrycznych, co często upraszcza rozwiązanie problemu.

1.2. Ruch po linii prostej

1.2.3. Graficzne obliczanie wielkości kinematycznych

Niektóre charakterystyki kinematyczne ruchu można obliczyć graficznie.

Definicja przewidywanej prędkości

Korzystając z wykresów zależności współrzędnej od czasu x (t) (lub drogi przebytej w czasie S (t)), możesz obliczyć odpowiednią projekcja prędkości v x w określonym momencie (ryc. 1.11), na przykład t = t 1.

Aby to zrobić, powinieneś:

1) zaznaczyć na osi czasu wskazaną wartość momentu czasu t 1;

2) przywrócić prostopadłość do przecięcia z wykresem x (t);

5) wyznaczyć rzut prędkości na oś Wółu jako tangens kąta stycznego do dodatniego kierunku osi czasu:

v x (t 1) = tan α 1 .

Należy zauważyć, że rzut prędkości v x wynosi

• dodatnia, jeśli styczna do wykresu tworzy kąt ostry z kierunkiem osi t (patrz rys. 1.11);
• ujemna, jeśli styczna do wykresu tworzy kąt rozwarty z kierunkiem osi t (ryc. 1.12).

Na ryc. Rysunek 1.12 przedstawia wykres współrzędnych w funkcji czasu x (t). Aby wyznaczyć rzut prędkości na oś Ox w chwili t 3, rysuje się prostopadłą t = t 3. W punkcie przecięcia prostopadłej z zależnością x (t) rysowana jest linia styczna. Tworzy kąt rozwarty z osią t. Zatem rzut prędkości v x na oś Ox we wskazanym czasie jest wartością ujemną:

v x (t 3) = - | tan α 3 | .

Ryż. 1.12

Definicja projekcji przyspieszenia

Korzystając z wykresu rzutu prędkości w funkcji czasu v x (t), można obliczyć rzut przyspieszenia a x na odpowiednią oś w określonym momencie (ryc. 1.13), np. t = t 2.

Aby to zrobić, powinieneś:

1) zaznaczyć na osi czasu wskazaną wartość momentu czasu t 2;

2) przywrócić prostopadłość do przecięcia z wykresem v x (t);

3) narysuj linię styczną do wykresu w miejscu jego przecięcia z prostopadłą;

5) wyznaczyć rzut przyspieszenia na oś Wółu jako tangens kąta stycznego do dodatniego kierunku osi czasu:

za x (t 2) = tan α 2 .

Należy zauważyć, że rzut przyspieszenia a x wynosi

• dodatnia, jeśli styczna do wykresu tworzy kąt ostry z kierunkiem osi t (patrz rys. 1.13);

Ryż. 1.13

• ujemna, jeśli styczna do wykresu tworzy kąt rozwarty z kierunkiem osi t (ryc. 1.14).

Ryż. 1.14

Wyjaśnienie zastosowania algorytmu. Na ryc. Rysunek 1.14 przedstawia wykres rzutowania prędkości w funkcji czasu v x (t). Aby wyznaczyć rzut przyspieszenia na oś Ox w chwili t 4, rysuje się prostopadłą t = t 4. W punkcie przecięcia prostopadłej z zależnością v x (t) rysowana jest linia styczna. Tworzy kąt rozwarty z osią t. Dlatego rzut przyspieszenia a x na oś Wółu w określonym czasie ma wartość ujemną:

za x (t 4) = - | tg α 4 | .

Wyznaczanie przebytej drogi i modułu przemieszczenia (połączenie ruchu jednostajnego i jednostajnie przyspieszonego)

Korzystając z wykresu rzutu prędkości w funkcji czasu v x (t), możesz obliczyć przebytą drogę i moduł podróżniczy punkt materialny (ciało) przez pewien okres czasu ∆t = t 2 - t 1 .

Aby obliczyć określone cechy, korzystając z wykresu zawierającego tylko przekroje równomiernie przyspieszony i ruch jednostajny, wygląda następująco:

4) obliczyć przebytą drogę S i moduł przemieszczenia ∆r jako sumy:

∆r = S 1 + S 2 + ... + S n,

gdzie S 1, S 2, ..., S n to ścieżki, po których przebywa punkt materialny w każdym z odcinków ruchu jednostajnie przyspieszonego i jednostajnego.

Na ryc. Rysunek 1.15 przedstawia zależność rzutu prędkości od czasu dla punktu materialnego (ciała) poruszającego się z przyspieszeniem jednostajnym na odcinku AB, jednostajnie na odcinku BC, równomiernie przyspieszonym na odcinku CD, ale z przyspieszeniem innym niż przyspieszenie na odcinku AB.

Ryż. 1,15

W tym przypadku przebyta droga S i moduł przemieszczenia ∆r pokrywają się i są obliczane ze wzorów:

S = S 1 + S 2 + S 3,

∆r = S 1 + S 2 + S 3,

gdzie S 1 jest drogą przebytą przez punkt materialny (ciało) w przekroju AB; S 2 - droga przebyta na odcinku BC; S 3 - droga przebyta na odcinku CD; S 1 , S 2 , S 3 oblicza się według algorytmu podanego powyżej.

Wyznaczanie przebytej drogi i modułu przemieszczenia (połączenie ruchu jednostajnego, równomiernie przyspieszonego i równomiernie opóźnionego)

Do obliczenia wskazanych charakterystyk wykorzystano wykres vx(t), zawierający przekroje nie tylko równomiernie przyspieszone i jednostajne, ale także równie powolny ruchu, powinieneś:

1) zaznaczyć na osi czasu zadany przedział czasu ∆t;

2) przywróć prostopadłe z punktów t = t 1 i t = t 2, aż przetną się z wykresem v x (t);

4) obliczyć przebytą drogę S jako sumę:

S = S 1 + S 2 + ... + S n,

gdzie S 1, S 2, ..., S n to ścieżki, po których przechodzi punkt materialny w każdym z odcinków;

5) obliczyć moduł podróżniczy jako różnica pomiędzy całkowitą drogą przebytą przez punkt materialny do punktu zatrzymania a drogą przebytą przez punkt materialny po zatrzymaniu.

Wyjaśnienie zastosowania algorytmu. Na ryc. Rysunek 1.16 przedstawia zależność prędkości od czasu punktu materialnego (ciała) poruszającego się z jednostajnym przyspieszeniem na odcinku AB, jednostajnie na odcinku BC i jednostajnie wolno na odcinku CF.

Ryż. 1.16

W przypadku, gdy mamy do czynienia z odcinkiem ruchu jednostajnie powolnego (zawierającym punkt zatrzymania – punkt D), przebyta droga S i moduł przemieszczenia ∆r nie pokrywają się. Przebytą odległość oblicza się ze wzoru

S = S 1 + S 2 + S 3 + S 4,

gdzie S 1 jest drogą przebytą przez punkt materialny (ciało) w przekroju AB; S 2 - droga przebyta na odcinku BC; S 3 - droga przebyta na odcinku CD; S 4 - droga przebyta na odcinku DF; S 1 , S 2 , S 3 , S 4 oblicza się według algorytmu podanego powyżej; Należy zauważyć, że wartość S 4 jest dodatnia.

Moduł przemieszczenia oblicza się ze wzoru

∆r = S 1 + S 2 + S 3 - S 4,

odejmując drogę przebytą przez punkt materialny (ciało) po obrocie.

Wyznaczanie modułu zmiany prędkości

Z wykresu rzutu przyspieszenia w funkcji czasu można znaleźć a x (t). moduł zmiany prędkości∆v punktu materialnego (ciała) w pewnym przedziale czasu ∆t = t 2 − t 1 (rys. 1.17).

Aby to zrobić, powinieneś:

1) zaznaczyć na osi czasu zadany przedział czasu ∆t;

2) przywróć prostopadłe z punktów t = t 1 i t = t 2, aż przetną się z wykresem a x (t);

4) obliczyć moduł zmiany prędkości w określonym przedziale czasu jako powierzchnię.

Przykład 4. Wykres rzutu prędkości pierwszego ciała na oś Wołu w funkcji czasu przedstawia linia prosta przechodząca przez punkty (0; 6) i (3; 0), druga - przez punkty ( 0; 0) i (8; 4), gdzie prędkość podawana jest w metrach na sekundę, czas - w sekundach. Ile razy różnią się moduły przyspieszenia pierwszego i drugiego ciała?

Rozwiązanie. Wykresy prognoz prędkości w funkcji czasu dla obu ciał pokazano na rysunku.

Rzut przyspieszenia pierwszego ciała definiuje się jako tangens kąta rozwartego α 1 ; jego moduł oblicza się ze wzoru

| x 1 | = | tan α 1 | = | tg (180 - α 3) | = 6 3 = 2 m/s 2.

Pierwsze ciało porusza się równie wolno; wielkość jego przyspieszenia wynosi a 1 = = 2 m/s 2.

Rzut przyspieszenia drugiego ciała definiuje się jako tangens kąta ostrego α 2 ; jego moduł oblicza się ze wzoru

a x 2 = tan α 2 = 4 8 = 0,5 m/s 2.

Drugie ciało porusza się ze stałym przyspieszeniem; wielkość jego przyspieszenia wynosi a 2 = 0,5 m/s 2.

Wymagany stosunek modułów przyspieszenia pierwszego i drugiego korpusu jest równy:

za 1 za 2 = 2 0,5 = 4 .

Przyspieszenie pierwszego ciała jest 4 razy większe niż przyspieszenie drugiego ciała.

Przykład 5. Wykres współrzędnej y w funkcji czasu dla pierwszego ciała przedstawiono jako linię prostą przechodzącą przez punkty (0; 0) i (5; 3), drugiego - przez punkty (3; 0) i (6; 6), gdzie współrzędne podaje się w metrach, czas w sekundach. Wyznacz stosunek modułów rzutów prędkości wskazanych ciał.

Rozwiązanie. Wykresy współrzędnej y w funkcji czasu dla obu ciał pokazano na rysunku.

Rzut prędkości pierwszego ciała definiuje się jako tangens kąta α 1; jego moduł oblicza się ze wzoru

v y 1 = tan α 1 = 3 5 = 0,6 m/s.

Rzut prędkości drugiego ciała definiuje się jako tangens kąta α 2; jego moduł oblicza się ze wzoru

v y 2 = tan α 2 = 6 3 = 2 m/s.

Obydwa rzuty prędkości mają znak dodatni; dlatego oba ciała poruszają się ze stałym przyspieszeniem.

Stosunek modułów rzutów prędkości wskazanych ciał wynosi:

| v y 2 | | v y 1 | = 2 0,6 ≈ 3 .

Wielkość rzutu prędkości drugiego ciała jest w przybliżeniu 3 razy większa niż wielkość rzutu prędkości drugiego ciała.

Przykład 6. Wykres zależności prędkości ciała od czasu przedstawiono jako linię prostą przechodzącą przez punkty (0; 4,0) i (2,5; 0), gdzie prędkość podana jest w metrach na sekundę, czas - w sekundy. Ile razy droga przebyta przez ciało jest większa od modułu przemieszczenia w ciągu 6,0 s ruchu?

Rozwiązanie. Na rysunku przedstawiono wykres zależności prędkości ciała od czasu. Punkt zatrzymania τ reszta = 2,5 s przypada w przedziale od 0 s do 6,0 s.

Zatem przebyta odległość jest sumą

S = S 1 + S 2,

a moduł przemieszczenia jest różnicą

| Δ r → | = | S 1 - S 2 | ,

gdzie S 1 jest drogą przebytą przez ciało w przedziale czasu od 0 s do 2,5 s; S 2 to droga przebyta przez ciało w przedziale czasu od 2,5 s do 6,0 s.

Wartości S 1 i S 2 obliczamy graficznie jako pola trójkątów pokazanych na rysunku:

S 1 = 1 2 ⋅ 4,0 ⋅ 2,5 = 5,0 m;

S 2 = 1 2 ⋅ (6,0 - 2,5) ⋅ 5,6 = 9,8 m.

Uwaga: wartość prędkości v = 5,6 m/s w chwili t = 6,0 s wynika z podobieństwa trójkątów, tj. od nastawienia

v 4,0 = 6,0 - 2,5 2,5 - 0 .

Obliczmy przebytą odległość:

S = S 1 + S 2 = 5,0 + 9,8 = 14,8 m

i ilość ruchu:

| Δ r → | = | S 1 - S 2 | = | 5,0 - 9,8 | = 4,8 m.

Znajdźmy wymagany stosunek przebytej drogi i modułu przemieszczenia:

S | Δ r → | = 14,8 4,8 ≈ 3,1.

Przebyta droga jest w przybliżeniu 3,1 razy większa od przemieszczenia.