Sebesség és gyorsulás vetületei. Mozgási sebesség A sebesség x tengelyre vetítésének modulja

Egy merev test két pontjának sebességének vetületei az ezeken a pontokon áthaladó tengelyre egyenlők egymással.
v A cos α = v B cos β.

Bizonyíték

Válasszunk egy téglalap alakú fix koordinátarendszert Oxyz. Vegyünk egy A és B merev test két tetszőleges pontját. Hadd (x A , y A , z A )És (x B , y B , z B )- ezen pontok koordinátái. Amikor egy merev test mozog, ezek a t idő függvényei. Az idő függvényében differenciálva megkapjuk a pontok sebességének vetületeit.
, .

Használjuk ki azt a tényt, hogy amikor egy merev test mozog, akkor a távolság | AB| pontok között állandó marad, azaz nem függ a t időtől. A távolság négyzete is állandó
.
Differenciáljuk ezt az egyenletet a t idő függvényében, alkalmazva a komplex függvény differenciálására vonatkozó szabályt.

Rövidítsük le 2 .
(1)

Bemutatjuk a vektort
.
Aztán az egyenlet (1) vektorok skaláris szorzataként ábrázolható.
(2)
Átalakításokat végzünk.
;
(3) .
A skaláris szorzattulajdonság szerint
,
.
Csere be (3) és csökkenteni kell | AB|.
;

Q.E.D.

Relatív sebesség

Tekintsük a B pont mozgását az A ponthoz képest. Vezessük be a B pont A-hoz viszonyított relatív sebességét.

Aztán az egyenlet (2) formában átírható
.

Vagyis a relatív sebesség merőleges az A pontból B pontba húzott vektorra. Mivel a B pontot tetszőlegesen vesszük, a merev test bármely pontjának relatív sebessége merőleges az A pontból húzott sugárvektorra. Vagyis az A ponthoz képest a test forgó mozgást végez. A testpontok relatív sebességét a forgó mozgás képlete határozza meg
.

Az A pontot, amelyhez képest a mozgást vizsgáljuk, gyakran nevezik pólus.

A B pont abszolút sebessége egy rögzített koordinátarendszerhez viszonyítva a következő formában írható fel:
.
Ez egyenlő egy tetszőleges A pont (pólus) transzlációs mozgási sebességének és az A pólushoz viszonyított forgási sebességének összegével.

Példa a probléma megoldására

A feladat

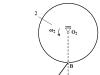
1-es és 2-es kerekek R sugarú 1 = 0,15 més R 2 = 0,3 m, illetve csuklópántokkal vannak összekötve egy 3 hosszúságú rúddal | AB| = 0,5 m. Az 1. kerék ω szögsebességgel forog 1 = 1 rad/s. Az ábrán látható mechanizmus helyzetéhez határozza meg az ω szögsebességet 2 kerekek 2. Vegyünk L = 0,3 m.

A probléma megoldása

Az A pont egy körben mozog sugár R 1 az O forgásközéppont körül 1 . Az A pont sebességét a képlet határozza meg
V A = ω 1 R 1.
A vektor függőlegesen van irányítva (merőlegesen O-ra 1 A).

A B pont körben mozog sugár R 2 az O forgásközéppont körül 2 . A B pont sebességét a képlet határozza meg
V B = ω 2 R 2.
Innen
.
A vektor vízszintesen irányul (merőlegesen O-ra 2 B).

Mi építkezünk derékszögű háromszög ABC. Alkalmazzuk a Pitagorasz-tételt.
(m)
.
A sebességvektor és az AB egyenes közötti szög koszinusza a vektor irányában egyenlő
.

Által sebességvetítési tétel egy merev test két pontja egy egyenesen:
V A cos α = V B cos β.
Innen
.

A 2. kerék szögsebességének meghatározása.
rad/s .

Egységes mozgás– ez állandó sebességű mozgás, vagyis amikor a sebesség nem változik (v = const) és nem történik gyorsulás vagy lassulás (a = 0).

Egyenes vonalú mozgás- ez az egyenes vonalú mozgás, vagyis az egyenes vonalú mozgás pályája egyenes.

Egyenletes lineáris mozgás- ez egy olyan mozgás, amelyben egy test egyenlő időközönként egyenlő mozgásokat végez. Például, ha egy bizonyos időintervallumot felosztunk egy másodperces intervallumokra, akkor egyenletes mozgással a test ugyanazt a távolságot fogja megtenni mindegyik időintervallumban.

Az egyenletes egyenes vonalú mozgás sebessége nem függ az időtől, és a pálya minden pontjában ugyanúgy irányul, mint a test mozgása. Azaz az elmozdulásvektor irányában egybeesik a sebességvektorral. Ebben az esetben az átlagos sebesség bármely időtartamra megegyezik a pillanatnyi sebességgel: v cp = v Egyenletes egyenes vonalú mozgás sebessége egy fizikai vektormennyiség, amely egyenlő a test bármely időtartam alatti mozgásának a t intervallum értékéhez viszonyított arányával:

Így az egyenletes egyenes vonalú mozgás sebessége megmutatja, hogy egy anyagi pont mekkora mozgást végez egységnyi idő alatt.

Mozgó Az egyenletes lineáris mozgást a következő képlet határozza meg:

Megtett távolság lineáris mozgásban egyenlő az eltolási modullal. Ha az OX tengely pozitív iránya egybeesik a mozgás irányával, akkor a sebesség vetülete az OX tengelyre egyenlő a sebesség nagyságával és pozitív:

V x = v, azaz v > 0 Az elmozdulás vetülete az OX tengelyre egyenlő: s = vt = x – x 0 ahol x 0 a test kezdeti koordinátája, x a test végső koordinátája (vagy a test koordinátája bármikor)

A mozgás egyenlete, azaz a test koordinátáinak függése az x = x(t) időtől a következő alakot ölti:

X = x 0 + vt Ha az OX tengely pozitív iránya ellentétes a test mozgási irányával, akkor a test sebességének vetülete az OX tengelyre negatív, a sebesség kisebb, mint nulla (v x = x 0 - vt

A sebesség, a koordináták és az út időfüggősége

ábra mutatja a testsebesség vetületének időfüggőségét. 1.11. Mivel a sebesség állandó (v = const), a sebességgrafikon az Ot időtengellyel párhuzamos egyenes.

Rizs. 1.11. A testsebesség vetületének időfüggősége az egyenletes egyenes vonalú mozgáshoz.

A mozgás vetülete a koordináta tengelyére számszerűen megegyezik az OABC téglalap területével (1.12. ábra), mivel a mozgásvektor nagysága egyenlő a sebességvektor és a mozgás időtartamának szorzatával. készült.

Rizs. 1.12. A test elmozdulásának vetületének időfüggősége az egyenletes egyenes vonalú mozgáshoz.

Az elmozdulás idő függvényében ábrázolt grafikonja az ábrán látható. 1.13. A grafikon azt mutatja, hogy a sebesség vetülete egyenlő

V = s 1 / t 1 = tan α ahol α a grafikonnak az időtengelyhez viszonyított dőlésszöge. Minél nagyobb az α szög, annál gyorsabban mozog a test, vagyis annál nagyobb a sebessége (annál nagyobb távolságot tesz meg a test rövidebb idő alatt). A koordináta és az idő grafikonjának érintője egyenlő a sebességgel: tg α = v

Rizs. 1.13. A test elmozdulásának vetületének időfüggősége az egyenletes egyenes vonalú mozgáshoz.

A koordináta időtől való függése az ábrán látható. 1.14. Az ábrából jól látszik, hogy

Tg α 1 > tan α 2 tehát az 1. test sebessége nagyobb, mint a 2. test sebessége (v 1 > v 2). tg α 3 = v 3 Ha a test nyugalomban van, akkor a koordináta gráf az időtengellyel párhuzamos egyenes, azaz x = x 0

Rizs. 1.14. A test koordinátáinak időfüggősége az egyenletes egyenes vonalú mozgáshoz.

A sebesség az egyik fő jellemző. Pontosan a mozgás lényegét fejezi ki, i.e. meghatározza az álló test és a mozgó test közötti különbséget.

A sebesség SI mértékegysége Kisasszony.

Fontos megjegyezni, hogy a sebesség vektormennyiség. A sebességvektor irányát a mozgás határozza meg. A sebességvektor mindig érintőlegesen irányul a pályára azon a ponton, amelyen a mozgó test áthalad (1. ábra).

Vegyük például egy mozgó autó kerekét. A kerék forog, és a kerék minden pontja körben mozog. A kerékről kiáramló fröccsenések ezeknek a köröknek az érintői mentén repülnek, jelezve a kerék egyes pontjainak sebességvektorainak irányát.

Így a sebesség egy test mozgási irányát (sebességvektor iránya) és mozgásának sebességét (sebességvektor modulusa) jellemzi.

Negatív sebesség

Lehet-e egy test sebessége negatív? Igen talán. Ha egy test sebessége negatív, ez azt jelenti, hogy a test a koordinátatengely irányával ellentétes irányba mozog a választott vonatkoztatási rendszerben. A 2. ábra egy busz és egy személygépkocsi mozgását mutatja. Az autó sebessége negatív, a buszé pedig pozitív. Emlékeztetni kell arra, hogy amikor a sebesség előjeléről beszélünk, akkor a sebességvektornak a koordináta tengelyére való vetületét értjük.

Egyenletes és egyenetlen mozgás

Általában a sebesség az időtől függ. A sebesség időfüggésének természete szerint a mozgás lehet egyenletes vagy egyenetlen.

MEGHATÁROZÁS

Egységes mozgás– ez egy állandó modulussebességű mozgás.

Egyenetlen mozgás esetén beszélünk:

Példák a „Sebesség” témával kapcsolatos problémák megoldására

1. PÉLDA

Gyakorlat	Az autó a két település közötti út első felét 90, a második felét 54 km/órás sebességgel tette meg. Határozza meg az autó átlagsebességét!
Megoldás	Helytelen lenne egy autó átlagsebességét a két jelzett sebesség számtani átlagaként kiszámítani. Használjuk az átlagsebesség definícióját: Mivel egyenes vonalú egyenletes mozgást feltételezünk, a vektorok előjelei elhagyhatók. Az autóval a teljes távolság megtételére fordított idő: ahol az út első felének teljesítésére fordított idő, és az út második felének teljesítésére fordított idő. A teljes mozgás egyenlő a lakott területek közötti távolsággal, azaz. . Ha ezeket az arányokat behelyettesítjük az átlagsebesség képletébe, a következőt kapjuk: Váltsuk át az egyes szakaszok sebességét SI rendszerbe: Ekkor az autó átlagsebessége: (Kisasszony)
Válasz	Az autó átlagsebessége 18,8 m/s

2. PÉLDA

Gyakorlat	Egy autó 10 másodpercig halad 10 m/s sebességgel, majd további 2 percig 25 m/s sebességgel halad. Határozza meg az autó átlagsebességét!
Megoldás	Készítsünk rajzot.

3.1. Egyenletes mozgás egyenes vonalban.

3.1.1. Egyenletes mozgás egyenes vonalban- egyenes vonalú mozgás nagyságrendi és irányú állandó gyorsulás mellett:

3.1.2. Gyorsulás()- egy fizikai vektormennyiség, amely megmutatja, hogy mennyit fog változni a sebesség 1 s alatt.

Vektoros formában:

ahol a test kezdeti sebessége, a test sebessége az adott pillanatban t.

A tengelyre vetítésben Ökör:

ahol a kezdeti sebesség vetülete a tengelyre Ökör, - a test sebességének vetítése a tengelyre Ökör egy adott időpontban t.

A vetületek előjele a vektorok irányától és a tengelytől függ Ökör.

3.1.3. A gyorsulás idő függvényében vetítési grafikonja.

Egyenletesen váltakozó mozgásnál a gyorsulás állandó, ezért az időtengellyel párhuzamos egyenesek formájában jelenik meg (lásd az ábrát):

3.1.4. Sebesség egyenletes mozgás közben.

Vektoros formában:

A tengelyre vetítésben Ökör:

Egyenletesen gyorsított mozgáshoz:

Az egyenletes lassítás érdekében:

3.1.5. Sebesség és idő vetületi grafikonja.

A sebesség és az idő vetületének grafikonja egy egyenes.

Mozgásirány: ha a grafikon (vagy annak egy része) az időtengely felett van, akkor a test a tengely pozitív irányában mozog Ökör.

Gyorsulási érték: minél nagyobb a dőlésszög tangense (minél meredekebben megy fel vagy le), annál nagyobb a gyorsulási modul; hol van a sebesség időbeli változása

Metszés az időtengellyel: ha a grafikon metszi az időtengelyt, akkor a metszéspont előtt a test lelassult (egyenletesen lassított), a metszéspont után pedig az ellenkező irányba gyorsulni kezdett (egyenletesen gyorsított mozgás).

3.1.6. A grafikon alatti terület geometriai jelentése a tengelyekben

A grafikon alatti terület a tengelyen Oy a sebesség késik, és a tengelyen Ökör- az idő a test által megtett út.

ábrán. A 3.5 az egyenletesen gyorsított mozgás esetét mutatja. Az út ebben az esetben megegyezik a trapéz területével: (3.9)

3.1.7. Képletek az útvonal kiszámításához

Egyenletesen gyorsított mozgás	Egyenlő lassítás
(3.10)	(3.12)
(3.11)	(3.13)
(3.14)

A táblázatban bemutatott összes képlet csak akkor működik, ha a mozgás iránya megmarad, vagyis addig, amíg az egyenes nem metszi az időtengelyt a sebesség vetülete az idő függvényében.

Ha a kereszteződés megtörtént, akkor a mozgás könnyebben két szakaszra osztható:

átkelés előtt (fékezés):

A kereszteződés után (gyorsítás, mozgás ellenkező irányba)

A fenti képletekben - a mozgás kezdetétől az időtengellyel való metszéspontig eltelt idő (megállás előtti idő), - az az út, amelyet a test megtett a mozgás kezdetétől az időtengellyel való metszéspontig, - az eltelt idő az időtengely átlépésének pillanatától e pillanatig t, - az az út, amelyet a test ellentétes irányban megtett az időtengely átlépésétől e pillanatig eltelt idő alatt t, - az elmozdulásvektor modulja a teljes mozgási időre, L- a test által a teljes mozgás során megtett út.

3.1.8. Mozgás a másodpercben.

Ezalatt a test a következő távolságot teszi meg:

Ezalatt a test a következő távolságot teszi meg:

Ekkor az intervallum alatt a test a következő távolságot teszi meg:

Bármely időtartamot intervallumnak vehetjük. Leggyakrabban azzal.

Ekkor a test 1 másodperc alatt a következő utat teszi meg:

2 másodperc múlva:

3 másodperc múlva:

Ha jól megnézzük, látni fogjuk, hogy stb.

Így a képlethez jutunk:

Szavakkal: a test által egymást követő időszakokban megtett utak páratlan számok sorozataként kapcsolódnak egymáshoz, és ez nem függ attól, hogy a test milyen gyorsulással mozog. Hangsúlyozzuk, hogy ez az összefüggés érvényes

3.1.9. A test koordinátáinak egyenlete az egyenletes mozgáshoz

Koordináta egyenlet

A kezdeti sebesség és a gyorsulás vetületeinek előjele a megfelelő vektorok és a tengely egymáshoz viszonyított helyzetétől függ Ökör.

A problémák megoldásához hozzá kell adni az egyenlethez a sebesség tengelyre való vetületének megváltoztatásának egyenletét:

3.2. Kinematikai mennyiségek grafikonjai egyenes vonalú mozgáshoz

3.3. Szabadesés test

Szabadesés alatt a következő fizikai modellt értjük:

1) Az esés a gravitáció hatására történik:

2) Nincs légellenállás (a problémákban néha azt írják, hogy „elhanyagolja a légellenállást”);

3) Minden test, függetlenül a tömegtől, ugyanolyan gyorsulással esik le (néha hozzáteszik, hogy „a test alakjától függetlenül”, de mi csak egy anyagi pont mozgását vesszük figyelembe, így a test alakja már nem veszi fel figyelembe);

4) A gravitáció gyorsulása szigorúan lefelé irányul, és egyenlő a Föld felszínén (a számítások megkönnyítése érdekében gyakran feltételezzük a problémákat);

3.3.1. A tengelyre vetített mozgásegyenletek Oy

Ellentétben a vízszintes egyenes mentén történő mozgással, amikor nem minden feladat jár mozgásirány-változtatással, szabadesésnél célszerű azonnal a tengelyre vetítésben felírt egyenleteket használni. Oy.

Test koordináta egyenlet:

Sebesség vetületi egyenlet:

Általános szabály, hogy problémák esetén kényelmes a tengely kiválasztása Oy a következő módon:

Tengely Oy függőlegesen felfelé irányítva;

Az origó egybeesik a Föld szintjével vagy a pálya legalacsonyabb pontjával.

Ezzel a választással a és egyenletek a következő formában íródnak át:

3.4. Mozgás egy síkban Oxy.

Egy test gyorsulással járó egyenes vonal menti mozgását vettük figyelembe. Az egyenletesen változó mozgás azonban nem korlátozódik erre. Például a vízszinteshez képest szögben bedobott test. Ilyen problémák esetén figyelembe kell venni a mozgást egyszerre két tengely mentén:

Vagy vektoros formában:

És a sebesség vetületének megváltoztatása mindkét tengelyen:

3.5. A derivált és integrál fogalmának alkalmazása

Itt nem adjuk meg a derivált és integrál részletes meghatározását. A problémák megoldásához csak egy kis képletkészletre van szükségünk.

Derivált:

Ahol A, B vagyis állandó értékek.

Integrál:

Most nézzük meg, hogyan vonatkozik a derivált és az integrál fogalma a fizikai mennyiségekre. A matematikában a deriváltot ""-vel jelöljük, a fizikában az időre vonatkozó deriváltot a függvény feletti "∙"-vel jelöljük.

Sebesség:

vagyis a sebesség a sugárvektor deriváltja.

Sebesség vetítéshez:

Gyorsulás:

vagyis a gyorsulás a sebesség deriváltja.

Gyorsulási vetítéshez:

Így ha ismerjük a mozgás törvényét, akkor könnyen megtaláljuk a test sebességét és gyorsulását is.

Most használjuk az integrál fogalmát.

Sebesség:

vagyis a sebességet a gyorsulás időintegráljaként találhatjuk meg.

Sugárvektor:

vagyis a sugárvektort a sebességfüggvény integráljának felvételével találhatjuk meg.

Így ha a függvény ismert, könnyen megtalálhatjuk a test sebességét és mozgástörvényét is.

A képletek állandóit a kezdeti feltételekből - értékekből és az idő pillanatában - határozzák meg

3.6. Sebességháromszög és eltolási háromszög

3.6.1. Sebesség háromszög

Állandó gyorsulású vektoros formában a sebességváltozás törvénye a következőképpen alakul: (3.5):

Ez a képlet azt jelenti, hogy egy vektor egyenlő a vektorok vektorösszegével, és a vektorösszeg mindig ábrázolható egy ábrán (lásd az ábrát).

Minden feladatban, a körülményektől függően, a sebességháromszögnek saját formája lesz. Ez az ábrázolás lehetővé teszi geometriai megfontolások alkalmazását a megoldásban, ami gyakran leegyszerűsíti a probléma megoldását.

3.6.2. A mozgások háromszöge

Vektor formában az állandó gyorsulással járó mozgás törvénye a következő:

Egy feladat megoldása során a legkényelmesebb módon választhatja ki a vonatkoztatási rendszert, ezért az általánosság elvesztése nélkül választhatjuk meg a vonatkoztatási rendszert úgy is, hogy a koordinátarendszer origóját arra a pontra helyezzük, ahol a test a kezdeti pillanatban helyezkedik el. Akkor

vagyis a vektor egyenlő a vektorok vektorösszegével és Ábrázoljuk az ábrán (lásd ábra).

Az előző esethez hasonlóan a körülményektől függően az eltolási háromszögnek saját alakja lesz. Ez az ábrázolás lehetővé teszi geometriai megfontolások alkalmazását a megoldásban, ami gyakran leegyszerűsíti a probléma megoldását.

1.2. Egyenes vonalú mozgás

1.2.3. Kinematikai mennyiségek grafikus számítása

A mozgás egyes kinematikai jellemzői grafikusan is kiszámíthatók.

A vetített sebesség definíciója

A koordináta x (t) időtől (vagy az S (t) időben megtett távolságtól) való függését ábrázoló grafikonok segítségével kiszámíthatja a megfelelő sebesség vetítés v x egy adott időpontban (1.11. ábra), például t = t 1.

Ehhez a következőket kell tennie:

1) jelölje be az időtengelyen a t 1 időpillanat jelzett értékét;

2) állítsa vissza az x (t) gráf metszéspontjának merőlegesét;

5) határozza meg a sebesség Ox tengelyre való vetületét az időtengely pozitív irányának érintőszögének érintőjeként:

v x (t 1) = tan α 1 .

Megjegyzendő, hogy a v x sebesség vetülete az

• pozitív, ha a grafikon érintője hegyesszöget zár be a t tengely irányával (lásd 1.11. ábra);
• negatív, ha a gráf érintője tompaszöget zár be a t tengely irányával (1.12. ábra).

ábrán. Az 1.12. ábra a koordináták grafikonját mutatja az x (t) idő függvényében. A sebesség t 3 időpontban az Ox tengelyre való vetületének meghatározásához t = t 3 merőlegest húzunk. A merőlegesnek az x (t) függőséggel való metszéspontjában egy érintővonalat húzunk. A t tengellyel tompaszöget zár be. Ezért a v x sebességnek az Ox tengelyre vetítése a jelzett időpontban negatív érték:

v x (t 3) = − | tan α 3 | .

Rizs. 1.12

A gyorsulási vetítés definíciója

A sebesség-vetület v x (t) idő függvényében ábrázolt grafikon segítségével kiszámítható a megfelelő tengelyen egy adott időpontban az a x gyorsulási vetület (1.13. ábra), például t = t 2.

Ehhez a következőket kell tennie:

1) jelölje be az időtengelyen a t 2 időpillanat jelzett értékét;

2) állítsa vissza a v x (t) gráf metszéspontjának merőlegesét;

3) rajzoljon egy érintőt a gráfra a merőleges metszéspontjában;

5) határozza meg a gyorsulás Ox tengelyre való vetületét az időtengely pozitív irányának érintőszögének érintőjeként:

a x (t 2) = tan α 2 .

Meg kell jegyezni, hogy az a x gyorsulás vetülete

• pozitív, ha a grafikon érintője hegyesszöget zár be a t tengely irányával (lásd 1.13. ábra);

Rizs. 1.13

• negatív, ha a gráf érintője a t tengely irányával tompaszöget zár be (1.14. ábra).

Rizs. 1.14

Az algoritmus használatának magyarázata.ábrán. Az 1.14. ábra a sebesség vetületének grafikonját mutatja az idő függvényében v x (t). A gyorsulás t 4 időpontban az Ox tengelyre való vetületének meghatározásához egy t = t 4 merőlegest húzunk. A v x (t) függőség merőleges metszéspontjában egy érintővonalat húzunk. A t tengellyel tompaszöget zár be. Ezért az a x gyorsulásnak az Ox tengelyre vetítése a megadott időpontban negatív érték:

a x (t 4) = − | tg α 4 | .

A megtett út és elmozdulás meghatározása modul (egyenletes és egyenletesen gyorsított mozgás kombinációja)

A sebességvetítés grafikonját használva v x (t) idő függvényében, kiszámítható a megtett távolság, ill. utazási modul anyagi pont (test) meghatározott ideig ∆t = t 2 − t 1 .

A megadott jellemzők kiszámítása csak szakaszokat tartalmazó grafikon segítségével egyenletesen gyorsulés egyenletes mozgás esetén a következő:

4) számítsa ki az S megtett távolságot és a ∆r elmozdulási modult összegként:

∆r = S 1 + S 2 + ... + S n,

ahol S 1, S 2, ..., S n az anyagi pont által bejárt utak az egyenletesen gyorsított és egyenletes mozgású szakaszokon.

ábrán. Az 1.15. ábra a sebességvetítés időfüggését mutatja egy anyagi pont (test) esetén, amely az AB szakaszon egyenletesen gyorsulva, a BC szakaszon egyenletesen, a CD szakaszon egyenletesen gyorsulva, de az AB szakaszban lévő gyorsulástól eltérő gyorsulással mozog.

Rizs. 1.15

Ebben az esetben az S megtett út és az ∆r eltolási modul egybeesik, és a következő képletekkel számítjuk ki:

S = S 1 + S 2 + S 3,

∆r = S 1 + S 2 + S 3,

ahol S 1 az AB szakaszban lévő anyagi pont (test) által megtett út; S 2 - a BC szakaszon megtett út; S 3 - megtett út a CD szakaszban; S 1 , S 2 , S 3 kiszámítása a fent megadott algoritmus szerint történik.

A megtett út és elmozdulás meghatározása modul (egyenletes, egyenletesen gyorsított és egyenletesen lassított mozgás kombinációja)

A jelzett jellemzők kiszámítása a v x (t) grafikon segítségével, amely nemcsak egyenletesen gyorsított és egyenletes metszeteket tartalmaz, hanem ugyanolyan lassú mozgás esetén:

1) jelölje be az időtengelyen a megadott ∆t időintervallumot;

2) állítsa vissza a merőlegeseket a t = t 1 és t = t 2 pontokból addig, amíg metszik a v x (t) gráfot;

4) számítsa ki az S megtett távolságot összegként:

S = S 1 + S 2 + ... + S n,

ahol S 1, S 2, ..., S n az egyes szakaszokon az anyagi pont által bejárt utak;

5) kiszámítani utazási modul mint az anyagi pont által a megállási pontig megtett teljes út és az anyagi pont által a megállás után megtett út különbsége.

Az algoritmus használatának magyarázata. ábrán. Az 1.16. ábra egy anyagi pont (test) sebességének időfüggőségét mutatja, amely az AB szakaszon egyenletesen gyorsulva, a BC szakaszon egyenletesen, a CF szakaszon egyenletesen lassan halad.

Rizs. 1.16

Abban az esetben, ha van egy egyenletesen lassított szakasz (beleértve a megállási pontot - D pont), akkor az S megtett út és az ∆r elmozdulási modul nem esik egybe. A megtett távolságot a képlet segítségével számítjuk ki

S = S 1 + S 2 + S 3 + S 4,

ahol S 1 az AB szakaszban lévő anyagi pont (test) által megtett út; S 2 - a BC szakaszon megtett út; S 3 - megtett út a CD szakaszban; S 4 - megtett út a DF szakaszban; Az S 1 , S 2 , S 3 , S 4 értékeket a fent megadott algoritmus szerint számítjuk ki; Megjegyzendő, hogy S 4 értéke pozitív.

Az eltolási modult a képlet segítségével számítjuk ki

∆r = S 1 + S 2 + S 3 − S 4,

levonva az anyagi pont (test) által megtett utat a forgatás után.

Sebességváltozási modulus meghatározása

A gyorsulás idő függvényében vetítésének grafikonján egy x (t) található sebességváltó modul Egy anyagi pont (test) ∆v egy bizonyos időintervallumra ∆t = t 2 − t 1 (1.17. ábra).

Ehhez a következőket kell tennie:

1) jelölje be az időtengelyen a megadott ∆t időintervallumot;

2) állítsa vissza a merőlegeseket a t = t 1 és t = t 2 pontokból addig, amíg nem metszik az a x (t) gráfot;

4) számítsa ki a sebesség változási modulusát a megadott időintervallumra mint területre.

4. példa: Az első test sebességének az Ox tengelyre vetítésének grafikonja az idő függvényében a (0; 6) és (3; 0) pontokon áthaladó egyenes vonallal, a második pedig a pontokon ( 0; 0) és (8; 4), ahol a sebesség méter per másodpercben, az idő másodpercben van megadva. Hányszor különbözik az első és a második test gyorsulási modulja?

Megoldás. Az ábrán mindkét test sebesség- és időbeli vetületeinek grafikonja látható.

Az első test gyorsulási vetületét az α 1 tompaszög érintőjeként határozzuk meg; a modulját a képlet számítja ki

| a x 1 | = | tan α 1 | = | tg (180 − α 3) | = 6 3 = 2 m/s 2.

Az első test ugyanolyan lassan mozog; gyorsulásának nagysága a 1 = = 2 m/s 2.

A második test gyorsulási vetületét az α 2 hegyesszög érintőjeként határozzuk meg; a modulját a képlet számítja ki

a x 2 = tan α 2 = 4 8 = 0,5 m/s 2.

A második test egyenletes gyorsulással mozog; gyorsulásának nagysága a 2 = 0,5 m/s 2.

Az első és a második test gyorsulási moduljainak szükséges aránya egyenlő:

a 1 a 2 = 2 0,5 = 4 .

Az első test gyorsulása 4-szer nagyobb, mint a második test gyorsulása.

5. példa: Az első test y-koordinátájának grafikonja az idő függvényében a (0; 0) és (5; 3) pontokon áthaladó egyenes vonalként, a második pedig a (3; 0) pontokon és (6; 6), ahol a koordináta méterben, az idő másodpercben van megadva. Határozza meg a jelzett testek sebességvetületei moduljainak arányát!

Megoldás. Az ábrán mindkét test y-koordinátájának grafikonja látható az idő függvényében.

Az első test sebességének vetülete az α 1 szög érintője; a modulját a képlet számítja ki

v y 1 = tan α 1 = 3 5 = 0,6 m/s.

A második test sebességének vetülete az α 2 szög érintője; a modulját a képlet számítja ki

v y 2 = tan α 2 = 6 3 = 2 m/s.

Mindkét sebességvetület pozitív előjelű; ezért mindkét test egyenletes gyorsulással mozog.

A jelzett testek sebességprojekcióinak moduljainak aránya:

| v y 2 | | v y 1 | = 2 0,6 ≈ 3 .

A második test sebességének vetületének nagysága körülbelül 3-szor nagyobb, mint a második test sebessége vetületének nagysága.

6. példa Egy test sebességének időfüggőségének grafikonját a (0; 4,0) és (2,5; 0) pontokon áthaladó egyenesként ábrázoljuk, ahol a sebesség méter per másodpercben van megadva, idő - másodpercek alatt. Hányszor nagyobb a test által megtett út, mint az elmozdulási modul 6,0 s mozgás alatt?

Megoldás. Az ábrán a testsebesség és az idő grafikonja látható. A τ rest = 2,5 s megállóhely a 0 s és 6,0 s közötti intervallumra esik.

Ezért a megtett távolság az összeg

S = S 1 + S 2,

és az eltolási modul a különbség

| Δ r → | = | S 1 − S 2 | ,

ahol S 1 a test által a 0 s és 2,5 s közötti időintervallum alatt megtett út; S 2 a test által 2,5 s és 6,0 s közötti időintervallumban megtett út.

Az S 1 és S 2 értékeit grafikusan számítjuk ki az ábrán látható háromszögek területeként:

S 1 = 1 2 ⋅ 4,0 ⋅ 2,5 = 5,0 m;

S 2 = 1 2 ⋅ (6,0 − 2,5) ⋅ 5,6 = 9,8 m.

Megjegyzés: a v = 5,6 m/s sebesség értékét a t = 6,0 s időpontban a háromszögek hasonlóságából kapjuk, azaz. hozzáállástól

v 4,0 = 6,0 - 2,5 2,5 - 0 .

Számítsuk ki a megtett távolságot:

S = S 1 + S 2 = 5,0 + 9,8 = 14,8 m

és a mozgás mennyisége:

| Δ r → | = | S 1 − S 2 | = | 5,0 – 9,8 | = 4,8 m.

Határozzuk meg a megtett út és az elmozdulás modul szükséges arányát:

S | Δ r → | = 14,8 4,8 ≈ 3,1.

A megtett út körülbelül 3,1-szerese az elmozdulásnak.