Projekcie rýchlosti a zrýchlenia. Rýchlosť pohybu Modul premietania rýchlosti na os x

Priemet rýchlostí dvoch bodov tuhého telesa na os prechádzajúcu týmito bodmi sú si navzájom rovné.
v A cos α = v b cos β.

Dôkaz

Vyberme si pravouhlý pevný súradnicový systém Oxyz. Zoberme si dva ľubovoľné body tuhého telesa A a B. Nechaj (x a, y a, z a) A (x b, y b, z b)- súradnice týchto bodov. Keď sa tuhé teleso pohybuje, sú funkciami času t. Diferencovaním podľa času získame projekcie rýchlostí bodov.
, .

Využime skutočnosť, že keď sa tuhé teleso pohybuje, vzdialenosť | AB | medzi bodmi zostáva konštantná, to znamená, že nezávisí od času t. Konštantná je aj druhá mocnina vzdialenosti
.
Diferencujme túto rovnicu vzhľadom na čas t, pričom použijeme pravidlo na derivovanie komplexnej funkcie.

Poďme to skrátiť 2 .
(1)

Predstavme si vektor
.
Potom rovnica (1) môže byť reprezentovaný ako skalárny súčin vektorov.
(2)
Vykonávame premeny.
;
(3) .
Podľa vlastnosti skalárneho produktu
,
.
Nahradiť v (3) a znížiť o | AB |.
;

Q.E.D.

Relatívna rýchlosť

Zvážte pohyb bodu B vzhľadom na bod A. Uveďme relatívnu rýchlosť bodu B vzhľadom na A.

Potom rovnica (2) možno prepísať do formy
.

To znamená, že relatívna rýchlosť je kolmá na vektor nakreslený z bodu A do bodu B. Keďže bod B sa berie ľubovoľne, relatívna rýchlosť ktoréhokoľvek bodu na tuhom telese je kolmá na vektor polomeru nakreslený z bodu A. To znamená, že vzhľadom na bod A teleso prechádza rotačným pohybom. Relatívna rýchlosť bodov tela je určená vzorcom pre rotačný pohyb
.

Často sa nazýva bod A, vzhľadom na ktorý sa uvažuje pohyb pól.

Absolútnu rýchlosť bodu B vzhľadom na pevný súradnicový systém možno zapísať v nasledujúcom tvare:
.
Rovná sa súčtu rýchlosti translačného pohybu ľubovoľného bodu A (pólu) a rýchlosti rotačného pohybu vzhľadom na pól A.

Príklad riešenia problému

Úloha

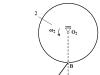
Kolesá 1 a 2 s polomerom R 1 = 0,15 m a R 2 = 0,3 m, respektíve sú spojené pántami s tyčou 3 dĺžok | AB| = 0,5 m. Koleso 1 sa otáča uhlovou rýchlosťou ω 1 = 1 rad/s. Pre polohu mechanizmu znázorneného na obrázku určte uhlovú rýchlosť ω 2 kolesá 2. Vezmite L = 0,3 m.

Riešenie problému

Bod A sa pohybuje v kruhu polomer R 1 okolo stredu otáčania O 1 . Rýchlosť bodu A je určená vzorcom
VA = ω 1 R 1.
Vektor je nasmerovaný vertikálne (kolmo na O 1 A).

Bod B sa pohybuje po kružnici polomer R 2 okolo stredu otáčania O 2 . Rýchlosť bodu B je určená vzorcom
VB = ω 2 R 2.
Odtiaľ
.
Vektor je nasmerovaný horizontálne (kolmo na O 2 B).

Строим správny trojuholník ABC. Aplikujeme Pytagorovu vetu.
(m)
.
Kosínus uhla medzi vektorom rýchlosti a priamkou AB v smere vektora sa rovná
.

Autor: teorém o projekcii rýchlosti dva body tuhého telesa na priamke máme:
V A cos α = V B cos β.
Odtiaľ
.

Zistenie uhlovej rýchlosti kolesa 2.
рад/с .

Равномерное движение– ide o pohyb konštantnou rýchlosťou, teda keď sa rýchlosť nemení (v = konštantná) a nedochádza k zrýchleniu alebo spomaleniu (a = 0).

Priamy pohyb- ide o pohyb po priamke, to znamená, že dráha priamočiareho pohybu je priamka.

Rovnomerný lineárny pohyb- ide o pohyb, pri ktorom telo robí rovnaké pohyby v ľubovoľných rovnakých časových intervaloch. Napríklad, ak rozdelíme určitý časový interval na jednosekundové intervaly, potom sa pri rovnomernom pohybe teleso posunie o rovnakú vzdialenosť pre každý z týchto časových intervalov.

Rýchlosť rovnomerného priamočiareho pohybu nezávisí od času a v každom bode trajektórie smeruje rovnako ako pohyb telesa. To znamená, že vektor posunutia sa zhoduje v smere s vektorom rýchlosti. V tomto prípade sa priemerná rýchlosť za akékoľvek časové obdobie rovná okamžitej rýchlosti: v cp = v Rýchlosť rovnomerného priamočiareho pohybu je fyzikálna vektorová veličina rovnajúca sa pomeru pohybu telesa za ľubovoľné časové obdobie k hodnote tohto intervalu t:

Rýchlosť rovnomerného priamočiareho pohybu teda ukazuje, koľko pohybu vykoná hmotný bod za jednotku času.

Sťahovanie s rovnomerným lineárnym pohybom je určený vzorcom:

Пройденный путь v lineárnom pohybe sa rovná modulu posunutia. Ak sa kladný smer osi OX zhoduje so smerom pohybu, potom sa priemet rýchlosti na os OX rovná veľkosti rýchlosti a je kladný:

V x = v, teda v > 0 Priemet posunutia na os OX sa rovná: s = vt = x – x 0 kde x 0 je počiatočná súradnica telesa, x je konečná súradnica telesa (alebo súradnice tela kedykoľvek)

Уравнение движения, teda závislosť súradníc telesa od času x = x(t), má tvar:

X = x 0 + vt Ak je kladný smer osi OX opačný k smeru pohybu telesa, potom je priemet rýchlosti telesa na os OX záporný, rýchlosť je menšia ako nula (v x = x 0 - VT

Závislosť rýchlosti, súradníc a dráhy od času

Závislosť priemetu rýchlosti telesa od času je znázornená na obr. 1.11. Keďže rýchlosť je konštantná (v = konštantná), graf rýchlosti je priamka rovnobežná s časovou osou Ot.

Ryža. 1.11. Závislosť priemetu rýchlosti telesa na čase pre rovnomerný priamočiary pohyb.

Priemet pohybu na súradnicovú os sa numericky rovná ploche obdĺžnika OABC (obr. 1.12), pretože veľkosť vektora pohybu sa rovná súčinu vektora rýchlosti a času, počas ktorého bol pohyb vyrobené.

Ryža. 1.12. Závislosť priemetu posunu telesa od času pre rovnomerný priamočiary pohyb.

Graf posunu v závislosti od času je znázornený na obr. 1.13. Graf ukazuje, že projekcia rýchlosti sa rovná

V = s 1 / t 1 = tan α kde α je uhol sklonu grafu k časovej osi. Čím väčší je uhol α, tým rýchlejšie sa teleso pohybuje, to znamená, že jeho rýchlosť je väčšia (čím dlhšiu vzdialenosť teleso prejde za kratší čas). Dotyčnica dotyčnice ku grafu súradnice v závislosti od času sa rovná rýchlosti: tg α = v

Ryža. 1.13. Závislosť priemetu posunu telesa od času pre rovnomerný priamočiary pohyb.

Závislosť súradnice od času je znázornená na obr. 1.14. Z obrázku je zrejmé, že

Tg α 1 > tan α 2 preto je rýchlosť telesa 1 vyššia ako rýchlosť telesa 2 (v 1 > v 2). tg α 3 = v 3 Ak je teleso v pokoji, potom súradnicový graf je priamka rovnobežná s časovou osou, teda x = x 0

Ryža. 1.14. Závislosť súradníc telesa na čase pre rovnomerný priamočiary pohyb.

Rýchlosť je jednou z hlavných charakteristík. Vyjadruje samotnú podstatu pohybu, t.j. určuje rozdiel, ktorý existuje medzi stacionárnym telesom a pohybujúcim sa telesom.

Jednotka rýchlosti SI je pani.

Je dôležité si uvedomiť, že rýchlosť je vektorová veličina. Smer vektora rýchlosti je určený pohybom. Vektor rýchlosti smeruje vždy tangenciálne k trajektórii v bode, ktorým prechádza pohybujúce sa teleso (obr. 1).

Vezmime si napríklad koleso idúceho auta. Koleso sa otáča a všetky body kolesa sa pohybujú v kruhoch. Špliechy odlietajúce z kolesa budú lietať pozdĺž dotyčníc k týmto kružniciam, pričom budú udávať smery vektorov rýchlosti jednotlivých bodov kolesa.

Rýchlosť teda charakterizuje smer pohybu telesa (smer vektora rýchlosti) a rýchlosť jeho pohybu (modul vektora rýchlosti).

Záporná rýchlosť

Môže byť rýchlosť telesa záporná? Áno možno. Ak je rýchlosť telesa záporná, znamená to, že sa teleso pohybuje v smere opačnom k ​​smeru súradnicovej osi vo zvolenom referenčnom systéme. Obrázok 2 znázorňuje pohyb autobusu a auta. Rýchlosť auta je záporná a rýchlosť autobusu kladná. Treba si uvedomiť, že keď hovoríme o značke rýchlosti, máme na mysli priemet vektora rýchlosti na súradnicovú os.

Rovnomerný a nerovnomerný pohyb

Vo všeobecnosti rýchlosť závisí od času. Podľa charakteru závislosti rýchlosti od času môže byť pohyb rovnomerný alebo nerovnomerný.

DEFINÍCIA

Равномерное движение– ide o pohyb s konštantnou modulovou rýchlosťou.

V prípade nerovnomerného pohybu hovoríme o:

Príklady riešenia problémov na tému „Rýchlosť“

PRÍKLAD 1

Cvičenie	Prvú polovicu cesty medzi dvoma osadami auto absolvovalo rýchlosťou 90 km/h, druhú polovicu rýchlosťou 54 km/h. Určte priemernú rýchlosť auta.
Riešenie	Bolo by nesprávne vypočítať priemernú rýchlosť auta ako aritmetický priemer dvoch uvedených rýchlostí. Použime definíciu priemernej rýchlosti: Keďže sa predpokladá priamočiary rovnomerný pohyb, znamienka vektorov možno vynechať. Čas strávený v aute na prejdenie celej vzdialenosti: kde je čas strávený dokončením prvej polovice cesty a čas strávený dokončením druhej polovice cesty. Celkový pohyb sa rovná vzdialenosti medzi obývanými oblasťami, t.j. . Nahradením týchto pomerov do vzorca pre priemernú rýchlosť dostaneme: Prepočítajme rýchlosti v jednotlivých úsekoch do sústavy SI: Potom je priemerná rýchlosť auta: (pani)
Odpoveď	Priemerná rýchlosť auta je 18,8 m/s

PRÍKLAD 2

Cvičenie	Auto ide 10 sekúnd rýchlosťou 10 m/s a potom ide ďalšie 2 minúty rýchlosťou 25 m/s. Určte priemernú rýchlosť auta.
Riešenie	Urobme si kresbu.

3.1. Rovnomerný pohyb v priamom smere.

3.1.1. Rovnomerný pohyb v priamom smere- pohyb v priamom smere s konštantným zrýchlením vo veľkosti a smere:

3.1.2. zrýchlenie()- fyzikálna vektorová veličina ukazujúca, ako veľmi sa zmení rýchlosť za 1 s.

Vo vektorovej forme:

kde je počiatočná rýchlosť telesa, je rýchlosť telesa v čase t.

V projekcii na os Vôl:

kde je priemet počiatočnej rýchlosti na os Vôl, - priemet rýchlosti telesa na os Vôl v určitom časovom bode t.

Znamienka projekcií závisia od smeru vektorov a osi Vôl.

3.1.3. Projekčný graf zrýchlenia v závislosti od času.

Pri rovnomernom striedavom pohybe je zrýchlenie konštantné, preto sa bude javiť ako priame čiary rovnobežné s časovou osou (pozri obrázok):

3.1.4. Rýchlosť pri rovnomernom pohybe.

Vo vektorovej forme:

V projekcii na os Vôl:

Pre rovnomerne zrýchlený pohyb:

Pre jednotný spomalený pohyb:

3.1.5. Projekčný graf závislosti rýchlosti od času.

Graf projekcie rýchlosti v závislosti od času je priamka.

Smer pohybu: ak je graf (alebo jeho časť) nad časovou osou, potom sa teleso pohybuje v kladnom smere osi Vôl.

Hodnota zrýchlenia: čím väčšia je dotyčnica uhla sklonu (čím strmšie stúpa alebo klesá), tým väčší je modul zrýchlenia; kde je zmena rýchlosti v čase

Priesečník s časovou osou: ak graf pretína časovú os, tak pred priesečníkom teleso spomalilo (rovnomerne spomalený pohyb) a za priesečníkom sa začalo zrýchľovať v opačnom smere (rovnomerne zrýchlený pohyb).

3.1.6. Geometrický význam plochy pod grafom v osiach

Oblasť pod grafom na osi Oj rýchlosť je oneskorená a na osi Vôl- čas je dráha, ktorou telo prechádza.

Na obr. 3.5 ukazuje prípad rovnomerne zrýchleného pohybu. Dráha sa v tomto prípade bude rovnať ploche lichobežníka: (3.9)

3.1.7. Vzorce na výpočet cesty

Rovnomerne zrýchlený pohyb	Rovnaký spomalený pohyb
(3.10)	(3.12)
(3.11)	(3.13)
(3.14)

Všetky vzorce uvedené v tabuľke fungujú iba vtedy, keď je zachovaný smer pohybu, to znamená, kým sa priamka nepretína s časovou osou na grafe projekcie rýchlosti v závislosti od času.

Ak došlo ku križovatke, pohyb je ľahšie rozdeliť do dvoch etáp:

pred prejazdom (brzdením):

Po križovatke (zrýchlenie, pohyb v opačnom smere)

Vo vzorcoch vyššie - čas od začiatku pohybu po priesečník s časovou osou (čas pred zastavením), - dráhu, ktorú teleso prešlo od začiatku pohybu po priesečník s časovou osou, - uplynulý čas od okamihu prekročenia časovej osi do tohto okamihu t, - dráhu, ktorú teleso prešlo v opačnom smere za čas, ktorý uplynul od okamihu prekročenia časovej osi do tohto okamihu t, - modul vektora posunu po celú dobu pohybu, L- dráha, ktorú telo prejde počas celého pohybu.

3.1.8. Pohyb v druhej sekunde.

Počas tejto doby telo prejde nasledujúcu vzdialenosť:

Počas tejto doby telo prejde nasledujúcu vzdialenosť:

Potom počas tohto intervalu telo prejde nasledujúcu vzdialenosť:

Akékoľvek časové obdobie možno považovať za interval. Najčastejšie s.

Potom telo prejde za 1 sekundu nasledujúcu vzdialenosť:

Za 2 sekundy:

Za 3 sekundy:

Ak sa pozorne pozrieme, uvidíme, že atď.

Dostávame sa teda k vzorcu:

Povedané slovami: dráhy, ktorými telo prechádza v po sebe nasledujúcich časových obdobiach, sú vo vzájomnom vzťahu ako séria nepárnych čísel, a to nezávisí od zrýchlenia, s ktorým sa teleso pohybuje. Zdôrazňujeme, že tento vzťah platí pre

3.1.9. Rovnica súradníc telesa pre rovnomerný pohyb

Уравнение координаты

Značky priemetov počiatočnej rýchlosti a zrýchlenia závisia od vzájomnej polohy zodpovedajúcich vektorov a osi Vôl.

Na vyriešenie problémov je potrebné do rovnice pridať rovnicu pre zmenu priemetu rýchlosti na os:

3.2. Grafy kinematických veličín pre priamočiary pohyb

3.3. Свободное падение тела

Voľným pádom rozumieme nasledujúci fyzikálny model:

1) K pádu dochádza pod vplyvom gravitácie:

2) Neexistuje žiadny odpor vzduchu (v problémoch niekedy píšu „zanedbať odpor vzduchu“);

3) Všetky telesá bez ohľadu na hmotnosť padajú s rovnakým zrýchlením (niekedy pridávajú „bez ohľadu na tvar telesa“, ale počítame s pohybom len hmotného bodu, takže tvar telesa sa už neberie do úvahy. do úvahy);

4) Gravitačné zrýchlenie smeruje striktne nadol a je rovnaké na povrchu Zeme (v problémoch, ktoré často predpokladáme pre pohodlie výpočtov);

3.3.1. Pohybové rovnice v priemete na os Oj

Na rozdiel od pohybu po vodorovnej priamke, keď nie všetky úlohy zahŕňajú zmenu smeru pohybu, pri voľnom páde je najlepšie okamžite použiť rovnice napísané v projekciách na os. Oj.

Telesná súradnicová rovnica:

Rovnica premietania rýchlosti:

Spravidla je v problémoch vhodné zvoliť os Ojследующим образом:

Os Oj nasmerované vertikálne nahor;

Počiatok sa zhoduje s úrovňou Zeme alebo najnižším bodom trajektórie.

Pri tejto voľbe sa rovnice a prepíšu do nasledujúceho tvaru:

3.4. Движение в плоскости Oxy.

Uvažovali sme o pohybe telesa so zrýchlením po priamke. Rovnomerne premenlivý pohyb však nie je obmedzený len na toto. Napríklad telo hodené pod uhlom k horizontále. В таких задачах необходимо учитывать движение сразу по двум осям:

Или в векторном виде:

И изменение проекции скорости на обе оси:

3.5. Применение понятия производной и интеграла

Мы не будем приводить здесь подробное определение производной и интеграла. Для решения задач нам понадобятся лишь небольшой набор формул.

odvodený:

Kde A, Bи то есть постоянные величины.

Integrálne:

Теперь посмотрим, как понятие производной и интеграла применимо к физическим величинам. V matematike sa derivácia značí """, vo fyzike sa derivácia vzhľadom na čas označí "∙" nad funkciou.

rýchlosť:

то есть скорость является производной от радиус-вектора.

Pre projekciu rýchlosti:

zrýchlenie:

то есть ускорение является производной от скорости.

Для проекции ускорения:

Ak je teda známy pohybový zákon, potom ľahko zistíme rýchlosť aj zrýchlenie telesa.

Теперь воспользуемся понятием интеграла.

rýchlosť:

to znamená, že rýchlosť možno nájsť ako časový integrál zrýchlenia.

Vektor polomeru:

to znamená, že vektor polomeru možno nájsť pomocou integrálu funkcie rýchlosti.

Ak je teda funkcia známa, ľahko nájdeme rýchlosť aj zákon pohybu telesa.

Konštanty vo vzorcoch sú určené z počiatočných podmienok - hodnôt a v čase

3.6. Треугольник скоростей и треугольник перемещений

3.6.1. Rýchlostný trojuholník

Vo vektorovej forme s konštantným zrýchlením má zákon zmeny rýchlosti tvar (3.5):

Tento vzorec znamená, že vektor sa rovná vektorovému súčtu vektorov a súčet vektorov môže byť vždy znázornený na obrázku (pozri obrázok).

V každom probléme, v závislosti od podmienok, bude mať rýchlostný trojuholník svoj vlastný tvar. Toto znázornenie umožňuje použitie geometrických úvah pri riešení, čo často zjednodušuje riešenie úlohy.

3.6.2. Trojuholník pohybov

Vo vektorovej forme má zákon pohybu s konštantným zrýchlením tvar:

Pri riešení úlohy si môžete zvoliť referenčný systém najvhodnejším spôsobom, preto bez straty všeobecnosti môžeme referenčný systém zvoliť tak, že počiatok súradnicového systému umiestnime do bodu, kde Telo sa nachádza v počiatočnom okamihu. Potom

to znamená, že vektor sa rovná vektorovému súčtu vektorov a znázornime ho na obrázku (pozri obrázok).

Rovnako ako v predchádzajúcom prípade, v závislosti od podmienok bude mať trojuholník posunutia svoj vlastný tvar. Toto znázornenie umožňuje použitie geometrických úvah pri riešení, čo často zjednodušuje riešenie úlohy.

1.2. Priamy pohyb

1.2.3. Grafický výpočet kinematických množstiev

Niektoré kinematické charakteristiky pohybu sa dajú vypočítať graficky.

Definícia premietanej rýchlosti

Pomocou grafov závislosti súradnice v čase x (t) (alebo vzdialenosť prejdená v čase s (t)), môžete vypočítať zodpovedajúci projekcia rýchlosti v x v určitom čase (obr. 1.11), napríklad t = t 1.

Ak to chcete urobiť, mali by ste:

1) Označte na časovej osi uvedená hodnota momentu času t 1;

2) obnoviť kolmo na priesečník s grafom x (t);

5) Stanovte projekciu rýchlosti na osi ox ako dotyčnica dotyčného uhla k pozitívnemu smeru časovej osi:

v x (t 1) = tan α 1.

Treba poznamenať, že projekcia rýchlosti v x je

• kladné, ak dotyčnica ku grafu zviera so smerom osi t ostrý uhol (pozri obr. 1.11);
• negatívne, ak dotyčnica ku grafu zviera so smerom osi t tupý uhol (obr. 1.12).

Na obr. Obrázok 1.12 ukazuje graf závislosti súradnice na čase x (t). Na určenie priemetu rýchlosti na os Ox v čase t 3 sa nakreslí kolmica t = t 3 . V priesečníku kolmice so závislosťou x (t) je nakreslená dotyčnica. S osou t zviera tupý uhol. Preto je projekcia rýchlosti v x na os Ox v uvedenom čase záporná:

v x (t 3) = − | tg α 3 | .

Ryža. 1.12

Определение проекции ускорения

Pomocou grafu projekcie rýchlosti od času v x (t) môžete vypočítať priemet zrýchlenia a x na príslušnej osi v určitom časovom bode (obr. 1.13), napríklad t = t 2.

Ak to chcete urobiť, mali by ste:

1) vyznačte na časovej osi udávanú hodnotu časového okamihu t 2;

2) восстановить перпендикуляр до пересечения с графиком v x (t );

3) провести к графику касательную линию в точке его пересечения с перпендикуляром;

5) určte priemet zrýchlenia na os Ox ako dotyčnicu uhla dotyčnice k kladnému smeru časovej osi:

a x (t2) = tan α2.

Следует отметить, что проекция ускорения a x является

• положительной , если касательная к графику образует острый угол с направлением оси t (см. рис. 1.13);

Ryža. 1.13

• отрицательной , если касательная к графику образует тупой угол с направлением оси t (рис. 1.14).

Ryža. 1.14

Пояснение к использованию алгоритма. Na obr. Obrázok 1.14 ukazuje graf projekcie rýchlosti v závislosti od času v x (t). Na určenie priemetu zrýchlenia na os Ox v čase t 4 sa nakreslí kolmica t = t 4 . V priesečníku kolmice so závislosťou v x (t) je nakreslená dotyčnica. Она образует тупой угол с осью t . Preto je projekcia zrýchlenia ax na os Ox v určenom čase záporná:

a x (t 4) = − | tg α 4 | .

Určenie prejdenej vzdialenosti a modul posunu (kombinácia rovnomerného a rovnomerne zrýchleného pohybu)

Pomocou grafu projekcie rýchlosti ako funkcie času v x (t) môžete vypočítať prejdenú vzdialenosť a cestovný modul hmotný bod (telo) za určitý časový úsek ∆t = t 2 − t 1 .

Na výpočet špecifikovaných charakteristík pomocou grafu obsahujúceho iba sekcie rovnomerne zrýchlenéи равномерного движения, следует:

4) vypočítajte prejdenú vzdialenosť S a modul posunutia ∆r ako súčty:

∆r = S 1 + S 2 + ... + S n ,

где S 1 , S 2 , ..., S n - пути, пройденные материальной точкой на каждом из участков равноускоренного и равномерного движения.

Na obr. Na obrázku 1.15 je znázornená závislosť projekcie rýchlosti od času pre hmotný bod (teleso), ktorý sa pohybuje rovnomerne zrýchlene v reze AB, rovnomerne v reze BC, rovnomerne zrýchlene v reze CD, ale so zrýchlením odlišným od zrýchlenia v reze AB.

Ryža. 1.15

В этом случае пройденный путь S и модуль перемещения ∆r совпадают и рассчитываются по формулам:

S = S1 + S2 + S3,

∆r = S 1 + S 2 + S 3,

где S 1 - путь, пройденный материальной точкой (телом) на участке AB ; S 2 - путь, пройденный на участке BC ; S 3 - путь, пройденный на участке CD ; S 1 , S 2 , S 3 рассчитываются по алгоритму, приведенному выше.

Určenie prejdenej vzdialenosti a modul posunu (kombinácia rovnomerného, ​​rovnomerne zrýchleného a rovnomerne spomaleného pohybu)

Na výpočet uvedených charakteristík pomocou grafu v x (t), ktorý obsahuje úseky nielen rovnomerne zrýchlených a rovnomerných, ale aj rovnako pomaly pohyb, mali by ste:

1) vyznačte na časovej osi špecifikovaný časový interval ∆t;

2) obnovte kolmice z bodov t = t 1 a t = t 2, kým sa nepretnú s grafom v x (t);

4) вычислить пройденный путь S как сумму:

S = S 1 + S 2 + ... + S n ,

kde S 1, S 2, ..., S n sú dráhy, ktoré prejde hmotný bod v každom z úsekov;

5) vypočítať cestovný modul ako rozdiel medzi celkovou dráhou prejdenú hmotným bodom do bodu zastavenia a dráhou, ktorú prejde hmotný bod po zastavení.

Пояснение к использованию алгоритма. Na obr. Obrázok 1.16 ukazuje závislosť rýchlosti od času pre hmotný bod (teleso), ktorý sa pohybuje rovnomerne zrýchlene v reze AB, rovnomerne v reze BC, rovnomerne pomaly v reze CF.

Ryža. 1.16

V prípade, že existuje úsek rovnomerne spomaleného pohybu (vrátane bodu zastavenia - bod D), prejdená vzdialenosť S a modul posunu ∆r sa nezhodujú. Prejdená vzdialenosť sa vypočíta pomocou vzorca

S = S 1 + S 2 + S 3 + S 4 ,

kde S 1 je dráha, ktorú prejde hmotný bod (teleso) v reze AB; S 2 - Cesta cestovala po sekcii BC; S 3 - Cesta cestovala na CD sekcie; S 4 - Cesta cestovala v oddiele DF; Si, S2, S3, S4 sa vypočítajú podľa algoritmu uvedeného vyššie; Treba poznamenať, že hodnota S 4 je kladná.

Modul posunu sa vypočíta pomocou vzorca

∆r = S 1 + S 2 + S 3 − S 4,

odpočítanie dráhy prejdenej hmotným bodom (telesom) po otočení.

Stanovenie modulu zmeny rýchlosti

Z grafu projekcie zrýchlenia od času a x (t) možno zistiť modul zmeny rýchlosti∆V materiálového bodu (telo) pre určitý časový interval ∆t = t2 - t 1 (obr. 1.17).

Ak to chcete urobiť, mali by ste:

1) vyznačte na časovej osi špecifikovaný časový interval ∆t;

2) Obnoviť kolmá z bodov t = t 1 a t = t2, kým sa nepretínajú s grafom a x (t);

4) Vypočítajte modul zmeny rýchlosti pre určený časový interval ako oblasť.

Príklad 4. Graf priemetu rýchlosti prvého telesa na os Ox v závislosti od času je znázornený priamkou prechádzajúcou bodmi (0; 6) a (3; 0), druhá - bodmi ( 0; 0) a (8; 4), kde je rýchlosť daná v metroch za sekundu, čas - v sekundách. Koľkokrát sa líšia moduly zrýchlenia prvého a druhého tela?

Riešenie. Grafy projekcií rýchlosti verzus čas pre obe telá sú znázornené na obrázku.

Projekcia zrýchlenia prvého tela je definovaná ako dotyčnica tupého uhla a 1; jeho modul sa vypočíta podľa vzorca

| a x 1 | = | tan α 1 | = | tg (180 − α 3) | = 63 = 2 m/s2.

Prvé teleso sa pohybuje rovnako pomaly; Veľkosť jeho zrýchlenia je 1 = = 2 m/s2.

Projekcia zrýchlenia druhého tela je definovaná ako dotyčnica akútneho uhla a2; jeho modul sa vypočíta podľa vzorca

a x 2 = tan α 2 = 4 8 = 0,5 m/s 2.

Druhé teleso sa pohybuje rovnomerným zrýchlením; Veľkosť jeho zrýchlenia je 2 = 0,5 m/s2.

Požadovaný pomer modulov zrýchlenia prvého a druhého tela sa rovná:

a 1 a 2 = 2 0,5 = 4 .

Zrýchlenie prvého tela je 4 -krát väčšie ako zrýchlenie druhého tela.

Príklad 5. Graf y-ovej súradnice v závislosti od času pre prvé teleso je znázornené ako priamka prechádzajúca bodmi (0; 0) a (5; 3), druhá - cez body (3; 0) a (6; 6), kde je súradnica daná v metroch, čas - v sekundách. Stanovte pomer modulov projekcií rýchlosti uvedených telies.

Riešenie. Na obrázku sú znázornené grafy y-koordinovaného v porovnaní s časom pre obe telá.

Priemet rýchlosti prvého telesa je definovaný ako dotyčnica uhla α 1; jeho modul sa vypočíta podľa vzorca

v y 1 = tan α 1 = 3 5 = 0,6 m/s.

Priemet rýchlosti druhého telesa je definovaný ako dotyčnica uhla α 2; jeho modul sa vypočíta podľa vzorca

v y 2 = tan α 2 = 6 3 = 2 m/s.

Obe projekcie rýchlosti majú kladné znamienko; preto sa obe telesá pohybujú rovnomerným zrýchlením.

Pomer modulov priemetov rýchlosti uvedených telies je:

| v y 2 | | v y 1 | = 2 0,6 ≈ 3.

Veľkosť priemetu rýchlosti druhého telesa je približne 3-krát väčšia ako veľkosť priemetu rýchlosti druhého telesa.

Príklad 6. Graf závislosti rýchlosti telesa od času je znázornený ako priamka prechádzajúca bodmi (0; 4,0) a (2,5; 0), kde rýchlosť je udávaná v metroch za sekundu, čas - v sekundách. Koľkokrát je vzdialenosť prejdená telesom väčšia ako modul posunutia za 6,0 s pohybu?

Riešenie. Graf závislosti rýchlosti tela od času je znázornený na obrázku. Bod zastavenia τ rest = 2,5 s spadá do intervalu od 0 s do 6,0 s.

Prejdená vzdialenosť je teda súčet

S = S1 + S2,

a modul posunutia je rozdiel

| Δ r → | = | S 1 − S 2 | ,

kde S 1 je dráha, ktorú teleso prejde za časový interval od 0 s do 2,5 s; S 2 je dráha, ktorú teleso prejde v časovom intervale od 2,5 s do 6,0 s.

Hodnoty S 1 a S 2 vypočítame graficky ako plochy trojuholníkov znázornených na obrázku:

S1 = 1 2 ⋅ 4,0 ⋅ 2,5 = 5,0 m;

S 2 = 1 2 ⋅ (6,0 − 2,5) ⋅ 5,6 = 9,8 m.

Poznámka: hodnotu rýchlosti v = 5,6 m/s v čase t = 6,0 s získame z podobnosti trojuholníkov, t.j. z postoja

v 4,0 = 6,0 − 2,5 2,5 − 0 .

Vypočítajme prejdenú vzdialenosť:

S = Si + S2 = 5,0 + 9,8 = 14,8 m

a množstvo pohybu:

| Δ r → | = | S 1 − S 2 | = | 5,0 − 9,8 | = 4,8 m.

Nájdite požadovaný pomer prejdenej vzdialenosti a modulu posunutia:

S | Δ r → | = 14,8 4,8 ≈ 3,1.

Prejdená vzdialenosť je približne 3,1-násobok výtlaku.