Proiectii ale vitezei si acceleratiei. Viteza de mișcare Modul de proiecție a vitezei pe axa x

Proiecțiile vitezelor a două puncte ale unui corp rigid pe o axă care trece prin aceste puncte sunt egale între ele.
vA cos α = v B cos β.

Dovada

Să alegem un sistem de coordonate dreptunghiular fix Oxyz. Să luăm două puncte arbitrare ale unui corp rigid A și B. Lăsa (x A , y A , z A )Și (x B , y B , z B )- coordonatele acestor puncte. Când un corp rigid se mișcă, acestea sunt funcții ale timpului t. Diferențiând în funcție de timp, obținem proiecții ale vitezelor punctelor.
, .

Să profităm de faptul că atunci când un corp rigid se mișcă, distanța | AB|între puncte rămâne constantă, adică nu depinde de timpul t. De asemenea, constant este pătratul distanței
.
Să diferențiem această ecuație în raport cu timpul t, aplicând regula de diferențiere a unei funcții complexe.

Să o scurtăm cu 2 .
(1)

Să introducem vectorul
.
Apoi ecuația (1) poate fi reprezentat ca produs scalar al vectorilor.
(2)
Efectuăm transformări.
;
(3) .
Prin proprietatea produsului scalar
,
.
Înlocuiește în (3) si reduce cu | AB|.
;

Q.E.D.

Viteza relativă

Luați în considerare mișcarea punctului B față de punctul A. Să introducem viteza relativă a punctului B în raport cu A.

Apoi ecuația (2) poate fi rescris sub formă
.

Adică, viteza relativă este perpendiculară pe vectorul desenat din punctul A în punctul B. Deoarece punctul B este luat în mod arbitrar, viteza relativă a oricărui punct de pe un corp rigid este perpendiculară pe vectorul rază desenat din punctul A. Adică, în raport cu punctul A, corpul suferă o mișcare de rotație. Viteza relativă a punctelor corpului este determinată de formula pentru mișcarea de rotație
.

Punctul A, în raport cu care este luată în considerare mișcarea, este adesea numit pol.

Viteza absolută a punctului B în raport cu un sistem de coordonate fix poate fi scrisă sub următoarea formă:
.
Este egală cu suma vitezei mișcării de translație a unui punct arbitrar A (pol) și a vitezei mișcării de rotație față de polul A.

Exemplu de rezolvare a problemei

Sarcina

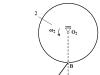
Roțile 1 și 2 cu raza R 1 = 0,15 mși R 2 = 0,3 m, respectiv, sunt legate prin balamale de o tijă de 3 lungimi | AB| = 0,5 m. Roata 1 se rotește cu viteza unghiulară ω 1 = 1 rad/s. Pentru poziția mecanismului prezentat în figură, determinați viteza unghiulară ω 2 roți 2. Luați L = 0,3 m.

Rezolvarea problemei

Punctul A se mișcă într-un cerc raza R 1 în jurul centrului de rotație O 1 . Viteza punctului A este determinată de formula
V A = ω 1 R 1.
Vectorul este îndreptat vertical (perpendicular pe O 1 A).

Punctul B se mișcă într-un cerc raza R 2 în jurul centrului de rotație O 2 . Viteza punctului B este determinată de formula
V B = ω 2 R 2.
De aici
.
Vectorul este îndreptat orizontal (perpendicular pe O 2 B).

Construim triunghi dreptunghic ABC. Aplicam teorema lui Pitagora.
(m)
.
Cosinusul unghiului dintre vectorul viteză și dreapta AB, în direcția vectorului, este egal cu
.

De teorema proiecției vitezei două puncte ale unui corp rigid pe o linie dreaptă avem:
V A cos α = V B cos β.
De aici
.

Aflarea vitezei unghiulare a roții 2.
rad/s .

Mișcare uniformă– aceasta este mișcarea cu o viteză constantă, adică atunci când viteza nu se modifică (v = const) și nu are loc accelerația sau decelerația (a = 0).

Mișcare în linie dreaptă- aceasta este mișcarea în linie dreaptă, adică traiectoria mișcării rectilinie este o linie dreaptă.

Mișcare liniară uniformă- aceasta este o mișcare în care un corp face mișcări egale la orice intervale de timp egale. De exemplu, dacă împărțim un anumit interval de timp în intervale de o secundă, atunci cu mișcare uniformă corpul se va deplasa la aceeași distanță pentru fiecare dintre aceste intervale de timp.

Viteza mișcării rectilinie uniforme nu depinde de timp și în fiecare punct al traiectoriei este direcționată în același mod ca și mișcarea corpului. Adică, vectorul deplasare coincide în direcție cu vectorul viteză. În acest caz, viteza medie pentru orice perioadă de timp este egală cu viteza instantanee: v cp = v Viteza mișcării rectilinie uniforme este o mărime vectorială fizică egală cu raportul dintre mișcarea unui corp în orice perioadă de timp și valoarea acestui interval t:

Astfel, viteza mișcării rectilinie uniforme arată cât de multă mișcare face un punct material pe unitatea de timp.

In miscare cu mișcare liniară uniformă este determinată de formula:

Distanta parcursaîn mișcare liniară este egală cu modulul de deplasare. Dacă direcția pozitivă a axei OX coincide cu direcția de mișcare, atunci proiecția vitezei pe axa OX este egală cu mărimea vitezei și este pozitivă:

V x = v, adică v > 0 Proiecția deplasării pe axa OX este egală cu: s = vt = x – x 0 unde x 0 este coordonata inițială a corpului, x este coordonata finală a corpului (sau coordonatele corpului în orice moment)

Ecuația mișcării, adică dependența coordonatelor corpului de timpul x = x(t), ia forma:

X = x 0 + vt Dacă direcția pozitivă a axei OX este opusă direcției de mișcare a corpului, atunci proiecția vitezei corpului pe axa OX este negativă, viteza este mai mică decât zero (v x = x 0 - vt

Dependența de viteză, coordonate și traseu în timp

Dependența proiecției vitezei corpului în timp este prezentată în Fig. 1.11. Deoarece viteza este constantă (v = const), graficul vitezei este o linie dreaptă paralelă cu axa timpului Ot.

Orez. 1.11. Dependența proiecției vitezei corpului în timp pentru mișcarea rectilinie uniformă.

Proiecția mișcării pe axa de coordonate este numeric egală cu aria dreptunghiului OABC (Fig. 1.12), deoarece mărimea vectorului de mișcare este egală cu produsul vectorului viteză și timpul în care a fost mișcarea. făcut.

Orez. 1.12. Dependența proiecției deplasării corpului în timp pentru mișcarea rectilinie uniformă.

Un grafic al deplasării în funcție de timp este prezentat în Fig. 1.13. Graficul arată că proiecția vitezei este egală cu

V = s 1 / t 1 = tan α unde α este unghiul de înclinare a graficului față de axa timpului. Cu cât unghiul α este mai mare, cu atât corpul se mișcă mai repede, adică cu atât viteza lui este mai mare (cu cât distanța parcurge corpul în mai puțin timp). Tangenta tangentei la graficul coordonatei în funcție de timp este egală cu viteza: tg α = v

Orez. 1.13. Dependența proiecției deplasării corpului în timp pentru mișcarea rectilinie uniformă.

Dependența coordonatei de timp este prezentată în Fig. 1.14. Din figură este clar că

Tg α 1 > tan α 2 prin urmare, viteza corpului 1 este mai mare decât viteza corpului 2 (v 1 > v 2). tg α 3 = v 3 Dacă corpul este în repaus, atunci graficul de coordonate este o dreaptă paralelă cu axa timpului, adică x = x 0

Orez. 1.14. Dependența coordonatelor corpului de timp pentru o mișcare rectilinie uniformă.

Viteza este una dintre principalele caracteristici. Ea exprimă însăși esența mișcării, adică. determină diferența care există între un corp staționar și un corp în mișcare.

Unitatea SI a vitezei este Domnișoară.

Este important să ne amintim că viteza este o mărime vectorială. Direcția vectorului viteză este determinată de mișcare. Vectorul viteză este întotdeauna direcționat tangențial la traiectoria în punctul prin care trece corpul în mișcare (Fig. 1).

De exemplu, luați în considerare roata unei mașini în mișcare. Roata se rotește și toate punctele roții se mișcă în cerc. Stropii care zboară de pe roată vor zbura de-a lungul tangentelor la aceste cercuri, indicând direcțiile vectorilor de viteză ai punctelor individuale ale roții.

Astfel, viteza caracterizează direcția de mișcare a unui corp (direcția vectorului viteză) și viteza mișcării acestuia (modulul vectorului viteză).

Viteza negativă

Poate fi viteza unui corp negativă? Da poate. Dacă viteza unui corp este negativă, aceasta înseamnă că corpul se mișcă în direcția opusă direcției axei de coordonate în sistemul de referință ales. Figura 2 prezintă mișcarea unui autobuz și a unei mașini. Viteza mașinii este negativă, iar viteza autobuzului este pozitivă. Trebuie amintit că atunci când vorbim despre semnul vitezei, ne referim la proiecția vectorului viteză pe axa de coordonate.

Mișcare uniformă și neuniformă

În general, viteza depinde de timp. În funcție de natura dependenței vitezei de timp, mișcarea poate fi uniformă sau neuniformă.

DEFINIȚIE

Mișcare uniformă– aceasta este mișcarea cu o viteză constantă a modulului.

În caz de mișcare neuniformă vorbim despre:

Exemple de rezolvare a problemelor pe tema „Viteză”

EXEMPLUL 1

Exercițiu	Mașina a parcurs prima jumătate a călătoriei între două localități cu o viteză de 90 km/h, iar a doua jumătate cu o viteză de 54 km/h. Determinați viteza medie a mașinii.
Soluţie	Ar fi incorect să se calculeze viteza medie a unei mașini ca medie aritmetică a celor două viteze indicate. Să folosim definiția vitezei medii: Deoarece se presupune o mișcare uniformă rectilinie, semnele vectorilor pot fi omise. Timpul petrecut de mașină pentru a parcurge întreaga distanță: unde este timpul petrecut pentru a parcurge prima jumătate a traseului și este timpul petrecut pentru a parcurge a doua jumătate a traseului. Mișcarea totală este egală cu distanța dintre zonele populate, adică. . Înlocuind aceste rapoarte în formula pentru viteza medie, obținem: Să convertim vitezele în secțiuni individuale în sistemul SI: Atunci viteza medie a mașinii este: (Domnișoară)
Răspuns	Viteza medie a mașinii este de 18,8 m/s

EXEMPLUL 2

Exercițiu	O mașină circulă timp de 10 secunde cu o viteză de 10 m/s și apoi conduce încă 2 minute cu o viteză de 25 m/s. Determinați viteza medie a mașinii.
Soluţie	Să facem un desen.

3.1. Mișcare uniformă în linie dreaptă.

3.1.1. Mișcare uniformă în linie dreaptă- mișcare în linie dreaptă cu accelerație constantă ca mărime și direcție:

3.1.2. Accelerare()- o mărime vectorială fizică care arată cât de mult se va schimba viteza în 1 s.

În formă vectorială:

unde este viteza inițială a corpului, este viteza corpului în momentul de timp t.

În proiecție pe axă Bou:

unde este proiecția vitezei inițiale pe axă Bou, - proiecția vitezei corpului pe axă Bou la un moment dat t.

Semnele proiecțiilor depind de direcția vectorilor și de axă Bou.

3.1.3. Graficul de proiecție al accelerației în funcție de timp.

Cu o mișcare alternativă uniformă, accelerația este constantă, de aceea va apărea ca linii drepte paralele cu axa timpului (vezi figura):

3.1.4. Viteza în timpul mișcării uniforme.

În formă vectorială:

În proiecție pe axă Bou:

Pentru o mișcare uniform accelerată:

Pentru o mișcare lentă uniformă:

3.1.5. Graficul de proiecție al vitezei în funcție de timp.

Graficul proiecției vitezei în funcție de timp este o linie dreaptă.

Direcția de mișcare: dacă graficul (sau o parte a acestuia) este deasupra axei timpului, atunci corpul se mișcă în direcția pozitivă a axei Bou.

Valoarea accelerației: cu cât tangenta unghiului de înclinare este mai mare (cu cât urcă sau coboară mai abruptă), cu atât modulul de accelerație este mai mare; unde este schimbarea vitezei în timp

Intersecția cu axa timpului: dacă graficul intersectează axa timpului, atunci înainte de punctul de intersecție corpul a încetinit (mișcare uniformă lentă), iar după punctul de intersecție a început să accelereze în direcția opusă (mișcare uniform accelerată).

3.1.6. Semnificația geometrică a zonei de sub grafic în axe

Aria de sub grafic când se află pe axă Oi viteza este intarziata, iar pe axa Bou- timpul este calea parcursă de corp.

În fig. 3.5 prezintă cazul mișcării uniform accelerate. Calea în acest caz va fi egală cu aria trapezului: (3.9)

3.1.7. Formule pentru calcularea traseului

Mișcare uniform accelerată	Mișcare lentă egală
(3.10)	(3.12)
(3.11)	(3.13)
(3.14)

Toate formulele prezentate în tabel funcționează numai atunci când se menține direcția de mișcare, adică până când linia dreaptă se intersectează cu axa timpului de pe graficul proiecției vitezei în funcție de timp.

Dacă intersecția a avut loc, atunci mișcarea este mai ușor de împărțit în două etape:

înainte de traversare (frânare):

După intersecție (accelerare, mișcare în sens opus)

În formulele de mai sus - timpul de la începutul mișcării până la intersecția cu axa timpului (timpul înainte de oprire), - calea pe care corpul a parcurs de la începutul mișcării până la intersecția cu axa timpului, - timpul scurs din momentul traversării axei timpului până în acest moment t, - traseul pe care corpul l-a parcurs în sens invers în timpul scurs din momentul traversării axei timpului până în acest moment t, - modulul vectorului deplasare pentru tot timpul de mișcare, L- traseul parcurs de corp pe parcursul intregii miscari.

3.1.8. Mișcare în a doua a doua.

În acest timp, corpul va parcurge următoarea distanță:

În acest timp, corpul va parcurge următoarea distanță:

Apoi, în timpul celui de-al treilea interval, corpul va parcurge următoarea distanță:

Orice perioadă de timp poate fi luată ca un interval. Cel mai adesea cu.

Apoi, în 1 secundă, corpul parcurge următoarea distanță:

In 2 secunde:

In 3 secunde:

Dacă ne uităm cu atenție, vom vedea că etc.

Astfel, ajungem la formula:

Cu cuvinte: traseele parcurse de un corp în perioade succesive de timp sunt legate între ele ca o serie de numere impare, iar aceasta nu depinde de accelerația cu care se mișcă corpul. Subliniem că această relație este valabilă pentru

3.1.9. Ecuația coordonatelor corpului pentru o mișcare uniformă

Ecuația de coordonate

Semnele proiecțiilor vitezei și accelerației inițiale depind de poziția relativă a vectorilor corespunzători și de axa Bou.

Pentru a rezolva probleme, este necesar să adăugați la ecuație ecuația pentru modificarea proiecției vitezei pe axă:

3.2. Grafice ale mărimilor cinematice pentru mișcarea rectilinie

3.3. Corpul în cădere liberă

Prin cădere liberă înțelegem următorul model fizic:

1) Căderea are loc sub influența gravitației:

2) Nu există rezistență la aer (în probleme se scrie uneori „neglijează rezistența aerului”);

3) Toate corpurile, indiferent de masă, cad cu aceeași accelerație (uneori se adaugă „indiferent de forma corpului”, dar luăm în considerare mișcarea doar a unui punct material, astfel încât forma corpului nu mai este luată în considerare);

4) Accelerația gravitației este îndreptată strict în jos și este egală pe suprafața Pământului (în problemele pe care le presupunem adesea pentru comoditatea calculelor);

3.3.1. Ecuații de mișcare în proiecție pe axă Oi

Spre deosebire de mișcarea de-a lungul unei linii drepte orizontale, când nu toate sarcinile implică o schimbare a direcției de mișcare, în cădere liberă este mai bine să folosiți imediat ecuațiile scrise în proiecții pe axă. Oi.

Ecuația coordonatelor corpului:

Ecuația de proiecție a vitezei:

De regulă, în probleme este convenabil să selectați axa Oi in felul urmator:

Axă Oiîndreptat vertical în sus;

Originea coincide cu nivelul Pământului sau cu punctul cel mai de jos al traiectoriei.

Cu această alegere, ecuațiile și vor fi rescrise în următoarea formă:

3.4. Mișcarea într-un avion Oxy.

Am luat în considerare mișcarea unui corp cu accelerație de-a lungul unei linii drepte. Cu toate acestea, mișcarea uniform variabilă nu se limitează la aceasta. De exemplu, un corp aruncat într-un unghi față de orizontală. În astfel de probleme, este necesar să se țină cont de mișcarea de-a lungul a două axe simultan:

Sau sub formă vectorială:

Și modificarea proiecției vitezei pe ambele axe:

3.5. Aplicarea conceptului de derivată și integrală

Nu vom oferi aici o definiție detaliată a derivatei și integralei. Pentru a rezolva probleme avem nevoie doar de un mic set de formule.

Derivat:

Unde A, Bși adică valori constante.

Integral:

Acum să vedem cum se aplică conceptele de derivată și integrală la mărimile fizice. În matematică, derivata se notează cu „””, în fizică, derivata în raport cu timpul se notează cu „∙” deasupra funcției.

Viteză:

adică viteza este o derivată a vectorului rază.

Pentru proiecția vitezei:

Accelerare:

adică accelerația este o derivată a vitezei.

Pentru proiecția accelerației:

Astfel, dacă legea mișcării este cunoscută, atunci putem găsi cu ușurință atât viteza, cât și accelerația corpului.

Acum să folosim conceptul de integrală.

Viteză:

adică viteza poate fi găsită ca integrală de timp a accelerației.

Vector rază:

adică vectorul rază poate fi găsit luând integrala funcției viteză.

Astfel, dacă funcția este cunoscută, putem găsi cu ușurință atât viteza, cât și legea mișcării corpului.

Constantele din formule sunt determinate din condițiile inițiale - valori și în momentul de timp

3.6. Triunghiul vitezei și triunghiul deplasării

3.6.1. Triunghiul vitezei

În formă vectorială cu accelerație constantă, legea schimbării vitezei are forma (3.5):

Această formulă înseamnă că un vector este egal cu suma vectorială a vectorilor, iar suma vectorială poate fi întotdeauna reprezentată într-o figură (vezi figura).

În fiecare problemă, în funcție de condiții, triunghiul vitezei va avea propria sa formă. Această reprezentare permite utilizarea unor considerații geometrice în soluție, ceea ce simplifică adesea rezolvarea problemei.

3.6.2. Triunghiul mișcărilor

În formă vectorială, legea mișcării cu accelerație constantă are forma:

Când rezolvați o problemă, puteți alege sistemul de referință în modul cel mai convenabil, prin urmare, fără a pierde generalitatea, putem alege sistemul de referință în așa fel încât, adică să plasăm originea sistemului de coordonate în punctul în care corpul este situat în momentul inițial. Apoi

adică vectorul este egal cu suma vectorială a vectorilor și Să-l reprezentăm în figură (vezi figura).

Ca și în cazul precedent, în funcție de condiții, triunghiul de deplasare va avea propria formă. Această reprezentare permite utilizarea unor considerații geometrice în soluție, ceea ce simplifică adesea rezolvarea problemei.

1.2. Mișcare în linie dreaptă

1.2.3. Calculul grafic al mărimilor cinematice

Unele caracteristici cinematice ale mișcării pot fi calculate grafic.

Definiția Projected Velocity

Folosind grafice ale dependenței coordonatei de timpul x (t) (sau distanța parcursă în timpul S (t)), puteți calcula proiecția vitezei v x la un anumit moment în timp (Fig. 1.11), de exemplu t = t 1.

Pentru a face acest lucru ar trebui:

1) marcați pe axa timpului valoarea indicată a momentului de timp t 1;

2) restabiliți perpendiculara pe intersecția cu graficul x (t);

5) determinați proiecția vitezei pe axa Ox ca tangentă a unghiului tangentei la direcția pozitivă a axei timpului:

v x (t 1) = tan α 1 .

Trebuie remarcat că proiecția vitezei v x este

• pozitiv dacă tangenta la grafic formează un unghi ascuțit cu direcția axei t (vezi Fig. 1.11);
• negativ dacă tangenta la grafic formează un unghi obtuz cu direcția axei t (fig. 1.12).

În fig. Figura 1.12 prezintă un grafic al coordonatei în funcție de timpul x (t). Pentru a determina proiecția vitezei pe axa Ox la momentul t 3, este trasată o perpendiculară t = t 3. În punctul de intersecție al perpendicularei cu dependența x (t) se trasează o linie tangentă. Formează un unghi obtuz cu axa t. Prin urmare, proiecția vitezei v x pe axa Ox la momentul indicat este o valoare negativă:

v x (t 3) = − | tan α 3 | .

Orez. 1.12

Definiţia Acceleration Projection

Folosind graficul proiecției vitezei în funcție de timp v x (t), puteți calcula proiecția accelerației a x pe axa corespunzătoare la un anumit moment în timp (Fig. 1.13), de exemplu t = t 2.

Pentru a face acest lucru ar trebui:

1) marcați pe axa timpului valoarea indicată a momentului de timp t 2;

2) restabiliți perpendiculara pe intersecția cu graficul v x (t);

3) trageți o linie tangentă la grafic în punctul de intersecție cu perpendiculara;

5) determinați proiecția accelerației pe axa Ox ca tangentă a unghiului tangentei la direcția pozitivă a axei timpului:

a x (t 2) = tan α 2 .

Trebuie remarcat faptul că proiecția accelerației a x este

• pozitiv dacă tangenta la grafic formează un unghi ascuțit cu direcția axei t (vezi Fig. 1.13);

Orez. 1.13

• negativ dacă tangenta la grafic formează un unghi obtuz cu direcția axei t (fig. 1.14).

Orez. 1.14

Explicația utilizării algoritmului.În fig. Figura 1.14 prezintă un grafic al proiecției vitezei în funcție de timp v x (t). Pentru a determina proiecția accelerației pe axa Ox la momentul t 4, este trasată o perpendiculară t = t 4. În punctul de intersecție al perpendicularei cu dependența v x (t) se trasează o linie tangentă. Formează un unghi obtuz cu axa t. Prin urmare, proiecția accelerației a x pe axa Ox la momentul specificat este o valoare negativă:

a x (t 4) = − | tg α 4 | .

Determinarea distanței parcurse și a modulului de deplasare (combinație de mișcare uniformă și uniform accelerată)

Folosind graficul proiecției vitezei în funcție de timpul v x (t), puteți calcula distanța parcursă și modul de călătorie punct material (corp) pentru o anumită perioadă de timp ∆t = t 2 − t 1 .

Pentru a calcula caracteristicile specificate folosind un grafic care conține numai secțiuni uniform acceleratși mișcare uniformă, urmează:

4) se calculează distanța parcursă S și modulul de deplasare ∆r ca sume:

∆r = S 1 + S 2 + ... + S n,

unde S 1, S 2, ..., S n sunt traseele parcurse de punctul material în fiecare dintre secțiunile de mișcare uniform accelerată și uniformă.

În fig. Figura 1.15 arată dependența proiecției vitezei în timp pentru un punct material (corp) care se deplasează uniform accelerat în secțiunea AB, uniform în secțiunea BC, uniform accelerat în secțiunea CD, dar cu o accelerație diferită de accelerația din secțiunea AB.

Orez. 1.15

În acest caz, distanța parcursă S și modulul de deplasare ∆r coincid și se calculează folosind formulele:

S = S 1 + S 2 + S 3,

∆r = S 1 + S 2 + S 3,

unde S 1 este calea parcursă de un punct material (corp) din secțiunea AB; S 2 - potecă parcursă pe tronsonul BC; S 3 - traseu parcurs în secţiunea CD; S1, S2, S3 sunt calculate conform algoritmului dat mai sus.

Determinarea distanței parcurse și a modulului de deplasare (combinație de mișcare uniformă, uniform accelerată și uniform decelerată)

Pentru a calcula caracteristicile indicate folosind graficul v x (t), care conține secțiuni nu numai uniform accelerate și uniforme, ci și la fel de lent mișcare, ar trebui să:

1) marcați intervalul de timp specificat ∆t pe axa timpului;

2) restabiliți perpendicularele din punctele t = t 1 și t = t 2 până când se intersectează cu graficul v x (t);

4) calculați distanța parcursă S ca sumă:

S = S 1 + S 2 + ... + S n,

unde S 1, S 2, ..., S n sunt traseele parcurse de punctul material în fiecare dintre secțiuni;

5) calculează modul de călătorie ca diferență între drumul total parcurs de punctul material până la punctul de oprire și drumul parcurs de punctul material după oprire.

Explicația utilizării algoritmului. În fig. Figura 1.16 arată dependența vitezei de timp pentru un punct material (corp) care se deplasează uniform accelerat în secțiunea AB, uniform în secțiunea BC, uniform lent în secțiunea CF.

Orez. 1.16

În cazul în care există o secțiune de mișcare uniformă lentă (inclusiv un punct de oprire - punctul D), distanța parcursă S și modulul de deplasare ∆r nu coincid. Distanța parcursă se calculează folosind formula

S = S 1 + S 2 + S 3 + S 4,

unde S 1 este calea parcursă de un punct material (corp) din secțiunea AB; S 2 - potecă parcursă pe tronsonul BC; S 3 - traseu parcurs în secţiunea CD; S 4 - traseu parcurs în tronsonul DF; S1, S2, S3, S4 sunt calculati conform algoritmului dat mai sus; Trebuie remarcat faptul că valoarea lui S 4 este pozitivă.

Modulul de deplasare se calculează folosind formula

∆r = S 1 + S 2 + S 3 − S 4,

scăzând drumul parcurs de punctul material (corpul) după rotație.

Determinarea modulului de schimbare a vitezei

Din graficul proiecției accelerației în funcție de timp a x (t) se poate găsi modul de schimbare a vitezei∆v al unui punct material (corp) pentru un anumit interval de timp ∆t = t 2 − t 1 (Fig. 1.17).

Pentru a face acest lucru ar trebui:

1) marcați intervalul de timp specificat ∆t pe axa timpului;

2) restabiliți perpendicularele din punctele t = t 1 și t = t 2 până când se intersectează cu graficul a x (t);

4) calculați modulul de modificare a vitezei pentru intervalul de timp specificat ca zonă.

Exemplul 4. Graficul proiecției vitezei primului corp pe axa Ox în funcție de timp este reprezentat de o linie dreaptă care trece prin punctele (0; 6) și (3; 0), al doilea - prin punctele ( 0; 0) și (8; 4), unde viteza este dată în metri pe secundă, timp - în secunde. De câte ori diferă modulele de accelerație ale primului și celui de-al doilea corp?

Soluţie. În figură sunt prezentate grafice ale proiecțiilor vitezei în funcție de timp pentru ambele corpuri.

Proiecția de accelerație a primului corp este definită ca tangenta unghiului obtuz α 1 ; modulul său se calculează prin formula

| a x 1 | = | tan α 1 | = | tg (180 − α 3) | = 6 3 = 2 m/s 2.

Primul corp se mișcă la fel de încet; mărimea accelerației sale este a 1 = = 2 m/s 2.

Proiecția de accelerație a celui de-al doilea corp este definită ca tangenta unghiului ascuțit α 2 ; modulul său se calculează prin formula

a x 2 = tan α 2 = 4 8 = 0,5 m/s 2.

Al doilea corp se mișcă cu o accelerație uniformă; magnitudinea accelerației sale este a 2 = 0,5 m/s 2.

Raportul necesar al modulelor de accelerație ale primului și celui de-al doilea corp este egal cu:

a 1 a 2 = 2 0,5 = 4 .

Accelerația primului corp este de 4 ori mai mare decât accelerația celui de-al doilea corp.

Exemplul 5. Graficul coordonatei y în funcție de timp pentru primul corp este reprezentat ca o linie dreaptă care trece prin punctele (0; 0) și (5; 3), al doilea - prin punctele (3; 0) și (6; 6), unde coordonatele sunt date în metri, timpul - în secunde. Determinați raportul modulelor proiecțiilor de viteză ale corpurilor indicate.

Soluţie. În figură sunt prezentate grafice ale coordonatei y în funcție de timp pentru ambele corpuri.

Proiecția vitezei primului corp este definită ca tangenta unghiului α 1; modulul său se calculează prin formula

v y 1 = tan α 1 = 3 5 = 0,6 m/s.

Proiecția vitezei celui de-al doilea corp este definită ca tangenta unghiului α 2; modulul său se calculează prin formula

v y 2 = tan α 2 = 6 3 = 2 m/s.

Ambele proiecții de viteză au semn pozitiv; prin urmare, ambele corpuri se deplasează cu o accelerație uniformă.

Raportul modulelor proiecțiilor de viteză ale corpurilor indicate este:

| v y 2 | | v y 1 | = 2 0,6 ≈ 3 .

Mărimea proiecției vitezei celui de-al doilea corp este de aproximativ 3 ori mai mare decât mărimea proiecției vitezei celui de-al doilea corp.

Exemplul 6. Graficul dependenței vitezei unui corp de timp este reprezentat ca o linie dreaptă care trece prin punctele (0; 4.0) și (2.5; 0), unde viteza este dată în metri pe secundă, timp - în secunde. De câte ori este distanța parcursă de corp mai mare decât modulul de deplasare în 6,0 s de mișcare?

Soluţie. În figură este prezentat un grafic al vitezei corpului în funcție de timp. Punctul de oprire τ repaus = 2,5 s scade în intervalul de la 0 s la 6,0 s.

Prin urmare, distanța parcursă este suma

S = S 1 + S 2,

iar modulul de deplasare este diferența

| Δ r → | = | S 1 − S 2 | ,

unde S 1 este calea parcursă de corp în intervalul de timp de la 0 s la 2,5 s; S 2 este calea parcursă de corp într-un interval de timp de la 2,5 s la 6,0 s.

Calculăm valorile lui S 1 și S 2 grafic ca zonele triunghiurilor prezentate în figură:

S 1 = 1 2 ⋅ 4,0 ⋅ 2,5 = 5,0 m;

S 2 = 1 2 ⋅ (6,0 − 2,5) ⋅ 5,6 = 9,8 m.

Notă: valoarea vitezei v = 5,6 m/s la momentul t = 6,0 s se obține din similitudinea triunghiurilor, adică. din atitudine

v 4,0 = 6,0 − 2,5 2,5 − 0 .

Să calculăm distanța parcursă:

S = S1 + S2 = 5,0 + 9,8 = 14,8 m

și cantitatea de mișcare:

| Δ r → | = | S 1 − S 2 | = | 5,0 − 9,8 | = 4,8 m.

Să găsim raportul necesar dintre distanța parcursă și modulul de deplasare:

S | Δ r → | = 14,8 4,8 ≈ 3,1.

Distanța parcursă este de aproximativ 3,1 ori deplasarea.