Greičio ir pagreičio projekcijos. Judėjimo greitis Greičio projekcijos į x ašį modulis

Dviejų standaus kūno taškų greičių projekcijos į ašį, einančią per šiuos taškus, yra lygios viena kitai.
prieš A cos α = v B cos β.

Įrodymas

Pasirinkime stačiakampę fiksuotų koordinačių sistemą Oxyz. Paimkime du savavališkus standaus kūno taškus A ir B. Leisti (x A , y A , z A ) Ir (x B , y B , z B )- šių taškų koordinatės. Kai standus kūnas juda, jie yra laiko t funkcijos. Diferencijuodami pagal laiką, gauname taškų greičių projekcijas.
, .

Pasinaudokime tuo, kad judant standžiam kūnui atstumas | AB| tarp taškų išlieka pastovus, tai yra nepriklauso nuo laiko t. Taip pat pastovus yra atstumo kvadratas
.
Išskirkime šią lygtį pagal laiką t, taikydami sudėtingos funkcijos diferencijavimo taisyklę.

Sutrumpinkime jį 2 .
(1)

Supažindinkime su vektoriumi
.
Tada lygtis (1) gali būti pavaizduotas kaip vektorių skaliarinė sandauga.
(2)
Atliekame transformacijas.
;
(3) .
Pagal skaliarinės sandaugos savybę
,
.
Pakeisti į (3) ir sumažinti iki | AB|.
;

Q.E.D.

Santykinis greitis

Apsvarstykite taško B judėjimą taško A atžvilgiu. Įveskime santykinį taško B greitį A atžvilgiu.

Tada lygtis (2) galima perrašyti į formą
.

Tai reiškia, kad santykinis greitis yra statmenas vektoriui, nubrėžtam iš taško A į tašką B. Kadangi taškas B imamas savavališkai, bet kurio standaus kūno taško santykinis greitis yra statmenas spindulio vektoriui, nubrėžtam iš taško A. Tai yra, taško A atžvilgiu kūnas patiria sukimosi judesį. Santykinis kūno taškų greitis nustatomas pagal sukimosi judesio formulę
.

Taškas A, kurio atžvilgiu nagrinėjamas judėjimas, dažnai vadinamas stulpas.

Absoliutus taško B greitis fiksuotos koordinačių sistemos atžvilgiu gali būti parašytas tokia forma:
.
Jis lygus savavališko taško A (poliaus) transliacinio judėjimo greičio ir sukimosi judėjimo greičio poliaus A atžvilgiu sumai.

Problemos sprendimo pavyzdys

Užduotis

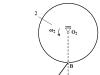
1 ir 2 ratai, kurių spindulys R 1 = 0,15 m ir R 2 = 0,3 m, atitinkamai, vyriais sujungti su 3 ilgių strypu | AB| = 0,5 m. 1 ratas sukasi kampiniu greičiu ω 1 = 1 rad/s. Paveiksle pavaizduotai mechanizmo padėčiai nustatykite kampinį greitį ω 2 ratai 2. Paimkite L = 0,3 m.

Problemos sprendimas

Taškas A juda apskritimu spindulys R 1 aplink sukimosi centrą O 1 . Taško A greitis nustatomas pagal formulę
V A = ω 1 R1.
Vektorius nukreiptas vertikaliai (statmenai O 1 A).

Taškas B juda apskritimu spindulys R 2 aplink sukimosi centrą O 2 . Taško B greitis nustatomas pagal formulę
V B = ω 2 R 2.
Iš čia
.
Vektorius nukreiptas horizontaliai (statmenai O 2 B).

Mes statome taisyklingas trikampis ABC. Taikome Pitagoro teoremą.
(m)
.
Kampo tarp greičio vektoriaus ir tiesės AB kosinusas vektoriaus kryptimi yra lygus
.

Autorius greičio projekcijos teorema turime du standaus kūno taškus tiesioje linijoje:
V A cos α = V B cos β.
Iš čia
.

2 rato kampinio greičio nustatymas.
rad/s .

Vienodas judėjimas– tai judėjimas pastoviu greičiu, tai yra, kai greitis nekinta (v = const) ir nevyksta pagreitis arba lėtėjimas (a = 0).

Tiesios linijos judėjimas- tai judėjimas tiesia linija, tai yra, tiesinio judėjimo trajektorija yra tiesi linija.

Vienodas linijinis judėjimas- tai judėjimas, kai kūnas atlieka vienodus judesius bet kokiais vienodais laiko intervalais. Pavyzdžiui, jei tam tikrą laiko intervalą padalinsime į vienos sekundės intervalus, tada vienodu judesiu kūnas judės tuo pačiu atstumu kiekvienam iš šių laiko intervalų.

Tolygaus tiesinio judėjimo greitis nepriklauso nuo laiko ir kiekviename trajektorijos taške yra nukreiptas taip pat, kaip ir kūno judėjimas. Tai yra, poslinkio vektorius sutampa su greičio vektoriumi. Šiuo atveju vidutinis greitis bet kuriuo laikotarpiu yra lygus momentiniam greičiui: v cp = v Vienodo tiesinio judėjimo greitis yra fizikinis vektorinis dydis, lygus kūno judėjimo per bet kurį laikotarpį santykiui su šio intervalo t reikšme:

Taigi tolygaus tiesinio judėjimo greitis parodo, kiek judesių per laiko vienetą atlieka materialus taškas.

Judėjimas su vienodu linijiniu judesiu nustatoma pagal formulę:

Nuvažiuotas atstumas tiesiniu judesiu yra lygus poslinkio moduliui. Jei teigiama OX ašies kryptis sutampa su judėjimo kryptimi, tada greičio projekcija į OX ašį yra lygi greičio dydžiui ir yra teigiama:

V x = v, tai yra v > 0 Poslinkio projekcija į OX ašį yra lygi: s = vt = x – x 0 kur x 0 yra pradinė kūno koordinatė, x yra galutinė kūno koordinatė (arba kūno koordinatės bet kuriuo metu)

Judėjimo lygtis, tai yra, kūno koordinačių priklausomybė nuo laiko x = x(t), yra tokia:

X = x 0 + vt Jei teigiama OX ašies kryptis yra priešinga kūno judėjimo krypčiai, tai kūno greičio projekcija į OX ašį yra neigiama, greitis mažesnis už nulį (v x = x 0 - vt

Greičio, koordinačių ir kelio priklausomybė nuo laiko

Kūno greičio projekcijos priklausomybė nuo laiko parodyta fig. 1.11. Kadangi greitis yra pastovus (v = const), greičio grafikas yra tiesė, lygiagreti laiko ašiai Ot.

Ryžiai. 1.11. Kūno greičio projekcijos priklausomybė nuo laiko vienodam tiesiniam judėjimui.

Judėjimo projekcija į koordinačių ašį skaitine prasme yra lygi stačiakampio OABC plotui (1.12 pav.), nes judėjimo vektoriaus dydis yra lygus greičio vektoriaus ir laiko, per kurį buvo atliktas judėjimas, sandaugai. pagamintas.

Ryžiai. 1.12. Kūno poslinkio projekcijos priklausomybė nuo laiko vienodam tiesiniam judėjimui.

Poslinkio ir laiko grafikas parodytas Fig. 1.13. Grafikas rodo, kad greičio projekcija lygi

V = s 1 / t 1 = tan α čia α yra grafiko pokrypio kampas į laiko ašį. Kuo didesnis kampas α, tuo kūnas greičiau juda, tai yra, tuo didesnis jo greitis (kuo ilgesnį atstumą kūnas įveikia per trumpesnį laiką). Koordinatės ir laiko grafiko liestinės liestinė yra lygi greičiui: tg α = v

Ryžiai. 1.13. Kūno poslinkio projekcijos priklausomybė nuo laiko vienodam tiesiniam judėjimui.

Koordinatės priklausomybė nuo laiko parodyta fig. 1.14. Iš paveikslo aišku, kad

Tg α 1 > tan α 2 todėl 1 kūno greitis yra didesnis nei 2 kūno greitis (v 1 > v 2). tg α 3 = v 3 Jei kūnas yra ramybės būsenoje, koordinačių grafikas yra tiesė, lygiagreti laiko ašiai, ty x = x 0

Ryžiai. 1.14. Kūno koordinačių priklausomybė nuo laiko vienodam tiesiniam judėjimui.

Greitis yra viena iš pagrindinių savybių. Ji išreiškia pačią judesio esmę, t.y. nustato skirtumą, kuris egzistuoja tarp nejudančio kūno ir judančio kūno.

SI greičio vienetas yra m/s.

Svarbu atsiminti, kad greitis yra vektorinis dydis. Greičio vektoriaus kryptį lemia judėjimas. Greičio vektorius visada nukreiptas liestinei trajektorijai taške, per kurį eina judantis kūnas (1 pav.).

Pavyzdžiui, apsvarstykite važiuojančio automobilio ratą. Ratas sukasi ir visi rato taškai juda apskritimais. Iš rato skrendantys purslai skris išilgai šių apskritimų liestinių, nurodydami atskirų rato taškų greičio vektorių kryptis.

Taigi greitis apibūdina kūno judėjimo kryptį (greičio vektoriaus kryptį) ir jo judėjimo greitį (greičio vektoriaus modulį).

Neigiamas greitis

Ar kūno greitis gali būti neigiamas? Taip galbūt. Jei kūno greitis yra neigiamas, tai reiškia, kad pasirinktoje atskaitos sistemoje kūnas juda priešinga koordinačių ašies krypčiai. 2 paveiksle parodytas autobuso ir automobilio judėjimas. Automobilio greitis neigiamas, o autobuso – teigiamas. Reikėtų prisiminti, kad kai kalbame apie greičio ženklą, turime omenyje greičio vektoriaus projekciją į koordinačių ašį.

Vienodas ir netolygus judėjimas

Apskritai greitis priklauso nuo laiko. Pagal greičio priklausomybės nuo laiko pobūdį judėjimas gali būti vienodas arba netolygus.

APIBRĖŽIMAS

Vienodas judėjimas– tai judėjimas pastoviu modulio greičiu.

Netolygaus judėjimo atveju kalbame apie:

Problemų sprendimo pavyzdžiai tema „Greitis“

1 PAVYZDYS

Pratimas	Pirmąją kelionės pusę tarp dviejų gyvenviečių automobilis įveikė 90 km/h greičiu, o antrąją pusę – 54 km/h greičiu. Nustatykite vidutinį automobilio greitį.
Sprendimas	Būtų neteisinga vidutinį automobilio greitį skaičiuoti kaip dviejų nurodytų greičių aritmetinį vidurkį. Naudokime vidutinio greičio apibrėžimą: Kadangi daroma prielaida, kad judesys yra vienodas, vektorių ženklų galima praleisti. Laikas, praleistas automobiliu įveikiant visą distanciją: kur yra laikas, praleistas įveikiant pirmąją kelio pusę, ir laikas, praleistas užbaigiant antrąją kelio pusę. Bendras judėjimas lygus atstumui tarp apgyvendintų vietovių, t.y. . Pakeitę šiuos santykius į vidutinio greičio formulę, gauname: Paverskime greitį atskirose atkarpose į SI sistemą: Tada vidutinis automobilio greitis yra: (m/s)
Atsakymas	Vidutinis automobilio greitis – 18,8 m/s

2 PAVYZDYS

Pratimas	Automobilis važiuoja 10 sekundžių 10 m/s greičiu, o po to dar 2 minutes važiuoja 25 m/s greičiu. Nustatykite vidutinį automobilio greitį.
Sprendimas	Padarykime piešinį.

3.1. Tolygus judėjimas tiesia linija.

3.1.1. Tolygus judėjimas tiesia linija- judėjimas tiesia linija, kurio pagreičio dydis ir kryptis yra pastovūs:

3.1.2. Pagreitis ()- fizinis vektorinis dydis, rodantis, kiek greitis pasikeis per 1 s.

Vektorine forma:

kur yra pradinis kūno greitis, yra kūno greitis laiko momentu t.

Projekcijoje į ašį Jautis:

kur yra pradinio greičio projekcija į ašį Jautis, - kūno greičio projekcija į ašį Jautis tam tikru momentu t.

Projekcijų ženklai priklauso nuo vektorių krypties ir ašies Jautis.

3.1.3. Pagreičio ir laiko projekcinis grafikas.

Esant tolygiai kintamam judėjimui, pagreitis yra pastovus, todėl jis atrodys kaip tiesios linijos, lygiagrečios laiko ašiai (žr. pav.):

3.1.4. Greitis vienodo judėjimo metu.

Vektorine forma:

Projekcijoje į ašį Jautis:

Tolygiai paspartintam judėjimui:

Norint užtikrinti vienodą sulėtintą judesį:

3.1.5. Greičio ir laiko projekcinis grafikas.

Greičio ir laiko projekcijos grafikas yra tiesi linija.

Judėjimo kryptis: jei grafikas (ar jo dalis) yra virš laiko ašies, tai kūnas juda teigiama ašies kryptimi Jautis.

Pagreičio reikšmė: kuo didesnė pasvirimo kampo tangentė (kuo statesnis kyla aukštyn arba žemyn), tuo didesnis pagreičio modulis; kur yra greičio pokytis laikui bėgant

Sankirta su laiko ašimi: jei grafikas kerta laiko ašį, tai prieš susikirtimo tašką kūnas sulėtėjo (tolygiai sulėtėjo), o po susikirtimo taško pradėjo greitėti priešinga kryptimi (tolygiai pagreitintas judėjimas).

3.1.6. Geometrinė ploto po grafiku reikšmė ašyse

Plotas po grafiku, kai yra ašyje Oy greitis atidėtas, o ašyje Jautis- laikas yra kūno nueitas kelias.

Fig. 3.5 parodytas tolygiai pagreitinto judėjimo atvejis. Kelias šiuo atveju bus lygus trapecijos plotui: (3.9)

3.1.7. Kelio skaičiavimo formulės

Tolygiai pagreitintas judesys	Vienodas sulėtintas judesys
(3.10)	(3.12)
(3.11)	(3.13)
(3.14)

Visos lentelėje pateiktos formulės veikia tik tada, kai išlaikoma judėjimo kryptis, tai yra, kol tiesė susikerta su laiko ašimi greičio projekcijos ir laiko grafike.

Jei susikirtimas įvyko, judėjimą lengviau suskirstyti į du etapus:

prieš pervažiuojant (stabdant):

Po sankryžos (pagreitis, judėjimas priešinga kryptimi)

Aukščiau pateiktose formulėse - laikas nuo judėjimo pradžios iki susikirtimo su laiko ašimi (laikas iki sustojimo), - kelias, kurį kūnas nuėjo nuo judėjimo pradžios iki sankirtos su laiko ašimi, - laikas, praėjęs. nuo laiko ašies kirtimo momento iki šio momento t, - kelias, kurį kūnas nuėjo priešinga kryptimi per laiką, praėjusį nuo laiko ašies kirtimo momento iki šio momento t, - poslinkio vektoriaus modulis visam judėjimo laikui, L- kūno nueitas kelias viso judėjimo metu.

3.1.8. Judėjimas sekundėje.

Per tą laiką kūnas nuvažiuos tokį atstumą:

Per tą laiką kūnas nuvažiuos tokį atstumą:

Tada per tąjį intervalą kūnas nuvažiuos tokį atstumą:

Bet koks laikotarpis gali būti laikomas intervalu. Dažniausiai su.

Tada per 1 sekundę kūnas nukeliauja tokį atstumą:

Per 2 sekundes:

Per 3 sekundes:

Jei atidžiai pažiūrėsime, pamatysime, kad ir t.

Taigi gauname formulę:

Žodžiais: kūno keliai, kuriuos eina vienas po kito einantys laikotarpiai, yra susiję vienas su kitu kaip nelyginių skaičių serija, ir tai nepriklauso nuo pagreičio, kuriuo kūnas juda. Pabrėžiame, kad šis santykis galioja

3.1.9. Kūno koordinačių lygtis vienodam judėjimui

Koordinačių lygtis

Pradinio greičio ir pagreičio projekcijų ženklai priklauso nuo atitinkamų vektorių santykinės padėties ir ašies Jautis.

Norint išspręsti problemas, prie lygties būtina pridėti greičio projekcijos į ašį keitimo lygtį:

3.2. Kinematinių dydžių grafikai tiesiniam judėjimui

3.3. Laisvo kritimo kūnas

Laisvas kritimas reiškia tokį fizinį modelį:

1) Kritimas įvyksta veikiant gravitacijai:

2) Nėra oro pasipriešinimo (problemose kartais rašoma „nepaisoma oro pasipriešinimo“);

3) Visi kūnai, nepriklausomai nuo masės, krenta tuo pačiu pagreičiu (kartais prideda „nepriklausomai nuo kūno formos“, bet mes svarstome tik materialaus taško judėjimą, todėl kūno forma nebepriimama atsižvelgti);

4) gravitacijos pagreitis nukreiptas griežtai žemyn ir yra lygus Žemės paviršiuje (problemose dažnai darome prielaidą, kad būtų patogiau skaičiuoti);

3.3.1. Judėjimo lygtys projekcijoje į ašį Oy

Skirtingai nuo judėjimo horizontalia tiesia linija, kai ne visos užduotys yra susijusios su judėjimo krypties pasikeitimu, laisvo kritimo metu geriausia iš karto naudoti lygtis, parašytas projekcijomis į ašį Oy.

Kūno koordinačių lygtis:

Greičio projekcijos lygtis:

Paprastai problemose patogu pasirinkti ašį Oy tokiu būdu:

Ašis Oy nukreipta vertikaliai į viršų;

Kilmė sutampa su Žemės lygiu arba žemiausiu trajektorijos tašku.

Pasirinkus šį pasirinkimą, ir lygtys bus perrašytos tokia forma:

3.4. Judėjimas plokštumoje Oxy.

Mes svarstėme kūno judėjimą su pagreičiu tiesia linija. Tačiau tolygiai kintamas judėjimas tuo neapsiriboja. Pavyzdžiui, kūnas, mestas kampu į horizontalę. Esant tokioms problemoms, būtina atsižvelgti į judėjimą išilgai dviejų ašių vienu metu:

Arba vektorine forma:

Ir keičiant greičio projekciją abiejose ašyse:

3.5. Išvestinės ir integralo sąvokos taikymas

Čia nepateiksime išsamaus išvestinės ir integralo apibrėžimo. Norėdami išspręsti problemas, mums reikia tik nedidelio formulių rinkinio.

Išvestinė:

Kur A, B o tai yra pastovios vertės.

Integruotas:

Dabar pažiūrėkime, kaip išvestinės ir integralo sąvokos taikomos fizikiniams dydžiams. Matematikoje išvestinė žymima „““, fizikoje išvestinė laiko atžvilgiu žymima „∙“ virš funkcijos.

Greitis:

tai yra, greitis yra spindulio vektoriaus išvestinė.

Greičio projekcijai:

Pagreitis:

tai pagreitis yra greičio išvestinė.

Pagreičio projekcijai:

Taigi, jei yra žinomas judėjimo dėsnis, galime nesunkiai rasti ir kūno greitį, ir pagreitį.

Dabar vartokime integralo sąvoką.

Greitis:

tai yra, greitį galima rasti kaip pagreičio laiko integralą.

Spindulio vektorius:

tai yra, spindulio vektorių galima rasti imant greičio funkcijos integralą.

Taigi, jei funkcija yra žinoma, galime nesunkiai rasti kūno greitį ir judėjimo dėsnį.

Konstantos formulėse nustatomos iš pradinių sąlygų - verčių ir laiko momentu

3.6. Greičio trikampis ir poslinkio trikampis

3.6.1. Greičio trikampis

Vektorinėje formoje su pastoviu pagreičiu greičio kitimo dėsnis turi tokią formą (3.5):

Ši formulė reiškia, kad vektorius yra lygus vektorių sumai ir vektorių sumą visada galima pavaizduoti paveiksle (žr. pav.).

Kiekvienoje užduotyje, priklausomai nuo sąlygų, greičio trikampis turės savo formą. Šis vaizdavimas leidžia sprendime naudoti geometrinius svarstymus, o tai dažnai supaprastina problemos sprendimą.

3.6.2. Judesių trikampis

Vektorinėje formoje judėjimo su pastoviu pagreičiu dėsnis turi tokią formą:

Sprendžiant uždavinį atskaitos sistemą galima pasirinkti patogiausiu būdu, todėl neprarasdami bendrumo, atskaitos sistemą galime pasirinkti taip, kad, tai yra, koordinačių sistemos pradžią patalpintume taške, kūnas yra pradiniu momentu. Tada

tai vektorius lygus vektorių sumai ir Pavaizduokime jį paveiksle (žr. pav.).

Kaip ir ankstesniu atveju, priklausomai nuo sąlygų, poslinkio trikampis turės savo formą. Šis vaizdavimas leidžia sprendime naudoti geometrinius svarstymus, o tai dažnai supaprastina problemos sprendimą.

1.2. Tiesios linijos judėjimas

1.2.3. Kinematinių dydžių grafinis skaičiavimas

Kai kurias kinematinės judėjimo charakteristikas galima apskaičiuoti grafiškai.

Prognozuojamo greičio apibrėžimas

Naudodami koordinatės priklausomybės nuo laiko x (t) grafikus (arba nuvažiuoto atstumo laiką S (t)), galite apskaičiuoti atitinkamą greičio projekcija v x tam tikru laiko momentu (1.11 pav.), pvz., t = t 1.

Norėdami tai padaryti, turėtumėte:

1) laiko ašyje pažymėkite nurodytą laiko momento reikšmę t 1;

2) atstatyti statmeną sankirtai su grafiku x (t);

5) nustatyti greičio projekciją į Ox ašį kaip liestinės kampo į teigiamą laiko ašies kryptį liestinę:

v x (t 1) = tan α 1 .

Pažymėtina, kad greičio v x projekcija yra

• teigiamas, jei grafiko liestinė sudaro smailųjį kampą su t ašies kryptimi (žr. 1.11 pav.);
• neigiamas, jei grafiko liestinė sudaro bukąjį kampą su t ašies kryptimi (1.12 pav.).

Fig. 1.12 paveiksle parodytas koordinačių ir laiko x (t) grafikas. Norint nustatyti greičio projekciją į Ox ašį momentu t 3, brėžiamas statmenas t = t 3. Statmens susikirtimo su priklausomybe x (t) taške brėžiama liestinė. Jis sudaro bukąjį kampą su t ašimi. Todėl greičio v x projekcija į Ox ašį nurodytu laiku yra neigiama reikšmė:

v x (t 3) = − | tan α 3 | .

Ryžiai. 1.12

Pagreičio projekcijos apibrėžimas

Naudodamiesi greičio projekcijos ir laiko v x (t) grafiku, galite apskaičiuoti pagreičio projekciją a x atitinkamoje ašyje tam tikru laiko momentu (1.13 pav.), pvz., t = t 2.

Norėdami tai padaryti, turėtumėte:

1) pažymėti laiko ašyje nurodytą laiko momento reikšmę t 2;

2) atstatyti statmeną sankirtai su grafiku v x (t);

3) nubrėžti grafiko liestinės liniją jo susikirtimo su statmenu taške;

5) nustatykite pagreičio projekciją į Ox ašį kaip liestinės kampo į teigiamą laiko ašies kryptį liestinę:

a x (t 2) = tan α 2 .

Reikia pažymėti, kad pagreičio a x projekcija yra

• teigiamas, jei grafiko liestinė sudaro smailųjį kampą su t ašies kryptimi (žr. 1.13 pav.);

Ryžiai. 1.13

• neigiamas, jei grafiko liestinė sudaro bukąjį kampą su t ašies kryptimi (1.14 pav.).

Ryžiai. 1.14

Algoritmo naudojimo paaiškinimas. Fig. 1.14 paveiksle parodytas greičio projekcijos ir laiko v x (t) grafikas. Norint nustatyti pagreičio projekciją į Ox ašį momentu t 4, brėžiamas statmuo t = t 4. Statmens susikirtimo su priklausomybe v x (t) taške brėžiama liestinė. Jis sudaro bukąjį kampą su t ašimi. Todėl pagreičio a x projekcija į Ox ašį nurodytu laiku yra neigiama reikšmė:

a x (t 4) = − | tg α 4 | .

Nuvažiuoto atstumo ir poslinkio nustatymas (vienodo ir tolygiai pagreitinto judesio derinys)

Naudodami greičio projekcijos grafiką kaip laiko funkciją v x (t), galite apskaičiuoti nuvažiuotą atstumą ir kelionių modulis materialus taškas (kūnas) tam tikram laikotarpiui ∆t = t 2 − t 1 .

Nurodytoms charakteristikoms apskaičiuoti naudojant grafiką, kuriame yra tik skyriai tolygiai pagreitintas ir tolygus judesys:

4) apskaičiuokite nuvažiuotą atstumą S ir poslinkio modulį ∆r kaip sumas:

∆r = S 1 + S 2 + ... + S n,

kur S 1, S 2, ..., S n yra materialaus taško einami takai kiekvienoje tolygiai pagreitinto ir vienodo judėjimo atkarpoje.

Fig. 1.15 paveiksle parodyta greičio projekcijos priklausomybė nuo laiko materialiam taškui (kūnui), judančiam tolygiai pagreitintai atkarpoje AB, tolygiai atkarpoje BC, tolygiai paspartintam atkarpoje CD, bet pagreičiu, kuris skiriasi nuo pagreičio AB ruože.

Ryžiai. 1.15

Šiuo atveju nuvažiuotas atstumas S ir poslinkio modulis ∆r sutampa ir apskaičiuojami pagal formules:

S = S 1 + S 2 + S 3,

∆r = S 1 + S 2 + S 3,

čia S 1 yra materialaus taško (kūno) atkarpoje AB nueitas kelias; S 2 - atkarpa BC nueitas kelias; S 3 - nueitas kelias atkarpoje CD; S 1 , S 2 , S 3 apskaičiuojami pagal aukščiau pateiktą algoritmą.

Nuvažiuoto atstumo ir poslinkio nustatymas (vienodo, tolygiai pagreitinto ir tolygiai lėtėjančio judėjimo derinys)

Nurodytas charakteristikas apskaičiuoti naudojant grafiką v x (t), kuriame yra ne tik tolygiai pagreitintos ir vienodos, bet ir vienodai lėtai judėjimą, turėtumėte:

1) laiko ašyje pažymėkite nurodytą laiko intervalą ∆t;

2) atkurkite statmenis iš taškų t = t 1 ir t = t 2, kol jie susikirs su grafiku v x (t);

4) apskaičiuokite nuvažiuotą atstumą S kaip sumą:

S = S 1 + S 2 + ... + S n,

čia S 1, S 2, ..., S n yra takai, kuriuos kerta materialus taškas kiekvienoje sekcijoje;

5) apskaičiuoti kelionių modulis kaip skirtumas tarp bendro kelio, kurį nukeliauja materialusis taškas iki sustojimo taško, ir kelio, kurį materialus taškas nueina sustojus.

Algoritmo naudojimo paaiškinimas. Fig. 1.16 paveiksle parodyta greičio priklausomybė nuo laiko, kai materialus taškas (kūnas) juda tolygiai greitai ruože AB, tolygiai atkarpoje BC, tolygiai lėtai ruože CF.

Ryžiai. 1.16

Tuo atveju, kai yra tolygiai lėto judėjimo atkarpa (įskaitant sustojimo tašką – tašką D), nuvažiuotas atstumas S ir poslinkio modulis ∆r nesutampa. Nuvažiuotas atstumas apskaičiuojamas pagal formulę

S = S 1 + S 2 + S 3 + S 4,

čia S 1 yra materialaus taško (kūno) atkarpoje AB nueitas kelias; S 2 - atkarpa BC nueitas kelias; S 3 - nueitas kelias atkarpoje CD; S 4 - atkarpoje DF nueitas kelias; S 1 , S 2 , S 3 , S 4 apskaičiuojami pagal aukščiau pateiktą algoritmą; Reikėtų pažymėti, kad S 4 reikšmė yra teigiama.

Poslinkio modulis apskaičiuojamas pagal formulę

∆r = S 1 + S 2 + S 3 − S 4,

atėmus materialaus taško (kūno) nueitą kelią po sukimosi.

Greičio kitimo modulio nustatymas

Iš pagreičio projekcijos laiko atžvilgiu grafiko galima rasti a x (t). greičio keitimo modulis Materialaus taško (kūno) ∆v tam tikram laiko intervalui ∆t = t 2 − t 1 (1.17 pav.).

Norėdami tai padaryti, turėtumėte:

1) laiko ašyje pažymėkite nurodytą laiko intervalą ∆t;

2) atkurkite statmenis iš taškų t = t 1 ir t = t 2, kol jie susikirs su grafiku a x (t);

4) apskaičiuoti greičio kitimo modulį nurodytam laiko intervalui kaip plotą.

4 pavyzdys. Pirmojo kūno greičio projekcijos į Ox ašį, palyginti su laiku, grafikas pavaizduotas tiesia linija, einančia per taškus (0; 6) ir (3; 0), antrosios - per taškus ( 0; 0) ir (8; 4), kur greitis nurodytas metrais per sekundę, laikas - sekundėmis. Kiek kartų skiriasi pirmojo ir antrojo kūno pagreičio moduliai?

Sprendimas. Abiejų kūnų greičio projekcijų ir laiko grafikai pateikti paveikslėlyje.

Pirmojo kūno pagreičio projekcija apibrėžiama kaip bukojo kampo α 1 liestinė; jo modulis apskaičiuojamas pagal formulę

| a x 1 | = | tan α 1 | = | tg (180 − α 3) | = 6 3 = 2 m/s 2.

Pirmasis kūnas juda vienodai lėtai; jo pagreičio dydis yra a 1 = = 2 m/s 2.

Antrojo kūno pagreičio projekcija apibrėžiama kaip smailiojo kampo α 2 liestinė; jo modulis apskaičiuojamas pagal formulę

a x 2 = tan α 2 = 4 8 = 0,5 m/s 2.

Antrasis kūnas juda vienodu pagreičiu; jo pagreičio dydis yra a 2 = 0,5 m/s 2.

Reikalingas pirmojo ir antrojo korpusų pagreičio modulių santykis yra lygus:

a 1 a 2 = 2 0,5 = 4 .

Pirmojo kūno pagreitis yra 4 kartus didesnis nei antrojo kūno pagreitis.

5 pavyzdys. Pirmojo kūno y koordinatės ir laiko grafikas pavaizduotas kaip tiesė, einanti per taškus (0; 0) ir (5; 3), antroji - per taškus (3; 0) ir (6; 6), kur koordinatė nurodyta metrais, laikas – sekundėmis. Nustatykite nurodytų kūnų greičio projekcijų modulių santykį.

Sprendimas. Abiejų kūnų y koordinatės ir laiko grafikai parodyti paveikslėlyje.

Pirmojo kūno greičio projekcija apibrėžiama kaip kampo α 1 liestinė; jo modulis apskaičiuojamas pagal formulę

v y 1 = tan α 1 = 3 5 = 0,6 m/s.

Antrojo kūno greičio projekcija apibrėžiama kaip kampo α 2 liestinė; jo modulis apskaičiuojamas pagal formulę

v y 2 = tan α 2 = 6 3 = 2 m/s.

Abi greičio projekcijos turi teigiamą ženklą; todėl abu kūnai juda vienodu pagreičiu.

Nurodytų kūnų greičio projekcijų modulių santykis yra:

| v y 2 | | v y 1 | = 2 0,6 ≈ 3 .

Antrojo kūno greičio projekcijos dydis yra maždaug 3 kartus didesnis nei antrojo kūno greičio projekcijos dydis.

6 pavyzdys. Kūno greičio priklausomybės nuo laiko grafikas pavaizduotas kaip tiesė, einanti per taškus (0; 4,0) ir (2,5; 0), kur greitis nurodytas metrais per sekundę, laikas - sekundėmis. Kiek kartų kūno nuvažiuotas atstumas yra didesnis už poslinkio modulį per 6,0 s judėjimo?

Sprendimas. Kūno greičio ir laiko grafikas parodytas paveikslėlyje. Sustojimo taškas τ poilsis = 2,5 s patenka į intervalą nuo 0 s iki 6,0 s.

Todėl nuvažiuotas atstumas yra suma

S = S 1 + S 2,

o poslinkio modulis yra skirtumas

| Δ r → | = | S 1 − S 2 | ,

kur S 1 – kūno nueitas kelias per laiko intervalą nuo 0 s iki 2,5 s; S 2 – kūno nueitas kelias per laiko intervalą nuo 2,5 s iki 6,0 s.

S 1 ir S 2 reikšmes apskaičiuojame grafiškai kaip trikampių plotus, parodytus paveikslėlyje:

S 1 = 1 2 ⋅ 4,0 ⋅ 2,5 = 5,0 m;

S 2 = 1 2 ⋅ (6,0 − 2,5) ⋅ 5,6 = 9,8 m.

Pastaba: greičio v = 5,6 m/s reikšmė momentu t = 6,0 s gaunama iš trikampių panašumo, t.y. nuo požiūrio

v 4,0 = 6,0 - 2,5 2,5 - 0 .

Apskaičiuokime nuvažiuotą atstumą:

S = S 1 + S 2 = 5,0 + 9,8 = 14,8 m

ir judesio kiekis:

| Δ r → | = | S 1 − S 2 | = | 5,0 – 9,8 | = 4,8 m.

Raskime reikiamą nuvažiuoto atstumo ir poslinkio modulio santykį:

S | Δ r → | = 14,8 4,8 ≈ 3,1.

Nuvažiuotas atstumas yra maždaug 3,1 karto didesnis už poslinkį.